Duas ondas de mesma frequência têm amplitudes e . As ondas interferem em um ponto no qual a diferença de fase é . Qual a amplitude resultante.
Passo 1
O problema menciona duas ondas com amplitudes diferentes e mesma frequência que interferem com uma defasagem de . As funções de onda podem ser escrita como
Onde,
Passo 2
Queremos somar as ondas usando o método dos fasores. Genericamente, temos a seguinte situação:
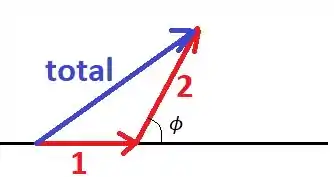
Note que a primeira função de onda está na direção horizontal, de modo que podemos escrever ela vetorialmente como
Já para a segunda função:
Somando as duas:
Passo 3
A amplitude resultante é obtida tomando o módulo de :
Desenvolvendo a expressão, encontramos
Portanto,
Logo,
Assim,