Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.3 - Ex. 30
Determine a soma das seguintes funções:
Passo 1
A questão fornece duas ondas de mesma frequência e quer que achemos a sua soma. As funções de onda podem ser escritas como
Onde,
Passo 2
Queremos somar as ondas usando o método dos fasores. Genericamente, temos a seguinte situação:
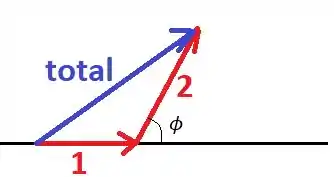
Note que a primeira função de onda está na direção horizontal, de modo que podemos escrever ela vetorialmente como
Já para a segunda função:
Somando as duas:
Passo 3
A amplitude resultante é obtida tomando o módulo de :
Desenvolvendo a expressão, encontramos
Portanto,
Logo,
Assim,
Passo 4
Sabemos que a função de onda resultante pode ser escrita como
onde é dado por
Portanto,
Assim, a função resultante será
Resposta
Exercícios de Livros Relacionados
No experimento da dupla fenda da Fig. 35-10, os campos elétricos das ondas que chegam ao ponto P são dados por E 1 = 2,00 μ V ms e n1,26 ⋅ 10 15t E 2 = 2,00 μ V ms e n1,26 ⋅ 10 15t + 39,6r a d onde o
Some as funções y_1 = 10 s e n omega t , y_2 = 15 s e n ( omega t + 30 ° ) e y_3 = 5,0 s e n ( omega t - 45 ° ) usando o método dos fasores.
Duas ondas de mesma frequência têm amplitudes 1,00 e 2,00 . As ondas interferem em um ponto no qual a diferença de fase é 60,0 ° . Qual a amplitude resultante.
Três ondas eletromagnéticas passam por um ponto P situado no eixo x . As ondas estão polarizadas paralelamente ao eixo y e as amplitudes dos campos elétricos são dadas pelas funções a seguir. Determin
62. A Figura 35.25 mostra um interferômetro denominado biprisma de Fresnel. O ângulo do prisma A é extremamente pequeno. a ) Se S 0 é uma fonte constituída por uma fenda muito estreita, mostre que a d