Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.3 - Ex. 31
Some as funções , e usando o método dos fasores.
Passo 1
O enunciado fornece três funções de onda que devemos somar usando o métodos dos fasores:
Representando essas três funções no diagram de fasores, obtemos
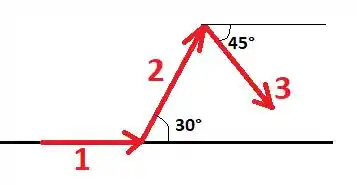
Passo 2
Para fazer a soma, decompomos os fasores nas direções e :
Assim, a amplitude será
Logo,
Já a fase será
Portanto,
Resposta
Exercícios de Livros Relacionados
Se o espelho M 2 de um interferômetro de Michaelson (Fig. 35-21) é deslocado de 0,233m m , a figura de interferência se desloca de 792 franjas claras. Qual é o comprimento de onda da luz responsável p
Até que distância deve se deslocar o espelho M 2 do interferômetro de Michelson (Figura 35.20) para que 1800 franjas da luz de um laser de He-Ne ( λ = 633n m ) se desloquem através de uma linha de ref
Jan inicialmente usa um interferômetro de Michelson com luz de 606n m proveniente de uma lâmpada de criptônio-86. Ele conta 818 franjas atravessando uma linha de referência no campo visual quando o es
61. O índice de refração de uma barra de vidro é 1,48 para uma temperatura T = 20 ° e varia linearmente com a temperatura, com um coeficiente de 2,50 ⋅ 10 - 5 / ° C . O coeficiente de dilatação linear
62. A Figura 35.25 mostra um interferômetro denominado biprisma de Fresnel. O ângulo do prisma A é extremamente pequeno. a ) Se S 0 é uma fonte constituída por uma fenda muito estreita, mostre que a d