Um elétron com fica em repouso depois de sofrer duas colisões com átomos como da fig. 40-14. Suponha que os átomos permanecem estacionários. O comprimento de onda do fóton emitido na segunda colisão é maior do que o comprimento de onda do fóton emitido na primeira colisão.
- Qual é a energia cinética do elétron apósa primeira colisão?
Determine
b) o comprimento de onda e
c) a energia do primeiro fóton.
Determine
d) o comprimento de onda e
e) a energia do segundo fóton.
Passo 1
Olá, tudo bem? Vou ajudar você nessa aqui! Sabemos que o comprimento de onda do primeiro fóton é e que o do segundo é , e que .
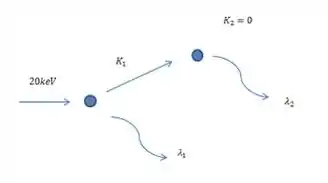 Sabemos também que a energia tem de ser conservada, certo? Então saca só esse esqueminha que fiz para entendermos melhor:
Sabemos também que a energia tem de ser conservada, certo? Então saca só esse esqueminha que fiz para entendermos melhor:
A energia inicial, vou chamar de deve ser igual à soma de e da energia do primeiro fóton . E também temos que a energia deve ser igual a energia mais a energia do segundo fóton. Como na segunda colisão o elétron fica em repouso, temos que .
Então da conservação de energia temos as seguintes equações:
E juntando essas duas equações temos:
Onde o valor de é .
Bom, agora precisamos resolver essa equação para e assim obter o valor de e determinar todas as quantidades que o problema pede, certo? Vamos lá?
Fazendo o mmc temos:
Ficamos com uma equação de segunda ordem em , vamos aplicar a fórmula de báskara:
Eu sei que ficou grande! Mas vamos usar uma calculadora, então vai ficar tudo bem!! Hihihi
E outra coisa, vamos usar só a raíz positiva, então só precisamos calcular isso uma vez:
E essa é a resposta do item . Vamos determonar já o item :
Passo 2
Letra c)
A energia do primeiro fóton é :
Passo 3
Letra d)
O comprimento de onda so segundo fóton é maior do que o primeiro. Como já calculamos , fica tranquilo determinar :
Passo 4
Letra e)
E sabendo o comprimento de onda do segundo fóton, podemos determinar a energia dele:
Mas já sabíamos disso, pois do passo temos:
Tranquilo até aqui? Vamos pra próxima então!