Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.Problemas Adicionais - Ex. 68
Um elétron se encontra no vácuo, perto da superfície da Terra, no ponto y = 0 de um eixo vertical. Qual deve ser a coordenada y de um segundo elétron situado no eixo y para que a força eletrostática exercida sobre o primeiro elétron compense o peso do primeiro elétron?
Passo 1
E aí, pessoal! 😁
O enunciado fala que tem um elétron no ponto e ele pede a posição de um segundo elétron para que a força eletrostática entre eles seja igual em módulo (porém com o sentido contrário) a força gravitacional. A força gravitacional sempre aponta para o centro da Terra. Consideraremos que a coordenada que o enunciado cita cresce para fora da superfície da Terra. Então a situação é mais o menos a seguinte:
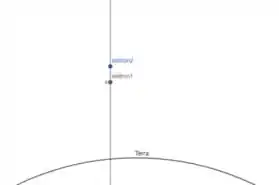
Então, nós devemos calcular o módulo da força gravitacional e eletrostática e igualar as duas 😊.
Para relembra a Lei de Coulomb:
E a força gravitacional:
Em que é a aceleração da gravidade, e são duas cargas (no caso do exercício, é a carga elementar, que é a carga de um elétron, , é a distância entre as duas cargas, que é o que queremos descobrir, é a constante de Coulomb ( e é a massa do elétron (.
Veja só! 😊
Passo 2
Substituindo os valores e igualando as forças, temos:
Assim, temos:
Como escolhemos o sentido crescente para cima, se o segundo elétron ficar em então a força eletrostática e a força gravitacional se anularam nele. Se escolhermos o sentido negativo, então a força eletrostática e a força gravitacional se anularão no elétron que está fixado em , que é o que o enunciado pede. O enunciado pede a posição do segundo elétron para que as forças se anulem no primeiro.
E aí! o que achou? Responde Aí!
