Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.11 - Ex. 59
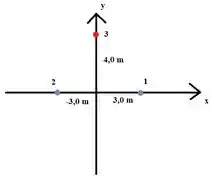
Duas cargas de 50 μC são mantidas fixas no eixo x nos pontos x = -3,0 m e x = 3,0 m. Uma partícula de carga q = -15 μC é liberada a partir do repouso em um ponto situado no semieixo y positivo. Devido à simetria da situação, a partícula se move ao longo do eixo y e possui uma energia cinética de 1,2 J ao passar pelo ponto x = 0, y = 4,0 m.
(a) Qual é a energia cinética da partícula ao passar pela origem?
(b) Para que valor negativo de y a partícula inverte o movimento?
Passo 1
Letra (a)
A questão pediu uma velocidade. Velocidade lembra energia cinética, e energia cinética lembra conservação da energia... e é isso que vamos fazer:
A energia potencial vai ficar nessa forma:
Por que não incluí a energia entre 1 e 2? Porque ela não muda. Não é?
Passo 2
Vamos substituir uns valores. Lembre que . Vamos chamar de q:
Substituindo os valores de K, e a gente chega a
Passo 3
Letra (b)
A partícula inverte o movimento quando ela para, certo? Então o que a gente tem que fazer é jogar a energia cinética final para zero:
A situação inicial aqui é aquela quando y = 4 m:
Invertendo os lados:
Substituindo os valores de K, e , achamos o valor de y:
Mas queremos o valor negativo, então:
Resposta
Letra (a): 3,0 J
Letra (b): -8,5 m