Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.11 - Ex. 41
Qual é o trabalho necessário para montar o arranjo da figura abaixo se q = 2,30 pC, a = 64,0 cm e as partículas estão inicialmente em repouso e infinitamente afastadas umas das outras?
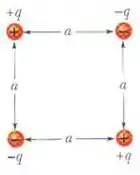
Passo 1
Nessa questão, queremos calcular o trabalho necessário para se montar o arranjo da figura, partindo do infinito até que fiquem na organização dada.
Sabendo que trabalho é a variação de energia mecânica, teremos:
No momento inicial, o enunciado nos dá que as partículas estão em repouso, logo e infinitamente afastadas, logo a energia potencial elétrica será nula também
Passo 2
Portanto, do que entendemos do passo anterior
Sendo assim, precisamos calcular a energia final, como as partículas no arranjo estão paradas, a energia cinética será zero e teremos apenas a potencial final
Para calcular a energia potencial elétrica de um sistema de partículas, a gente tem que calcular a energia de todos os pares de carga e somar tudo, usando a fórmula:
Vamos começar analisando quantos pares temos, e aqui será importante o sinal de cada par.
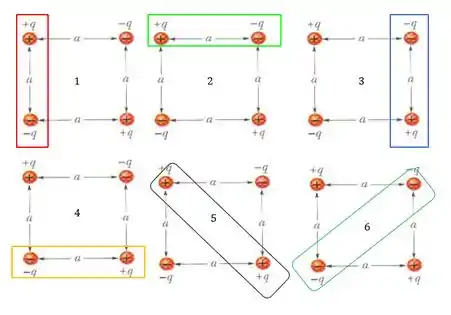
Na figura, temos 6 pares possíveis, 4 com distância e 2 com distância , que são os que estão opostos pelas diagonais do quadrado. Vamos combinar os pares de cargas possíveis e soma-los.
Passo 3
Agora vamos combinar todos aqueles pares que vimos, não esquecendo do sinal ok? Já te digo aqui que todos os pares que não estão na diagonal terão sinal negativo pois suas cargas são diferentes, e os que estão opostos pelo vértice serão positivos, teremos então:
Podemos colocar em evidência pra deixar mais bonitinho isso aqui
Passo 4
Agora é só substituir os valores de , e que teremos:
E lembrando que o trabalho é exatamente essa energia que calculamos: