Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 19.1 - Ex. 17
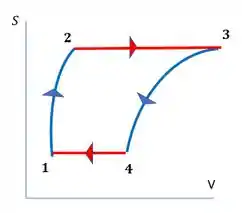
Esboce um diagrama SV para o ciclo de Carnot com um gás ideal.
Passo 1
Olá! Então, ele quer que a gente faça o diagrama SV (entropia versus volume) do ciclo de Carnot.
Legal galera, vamos começar relembrando o ciclo de Carnot e suas etapas.
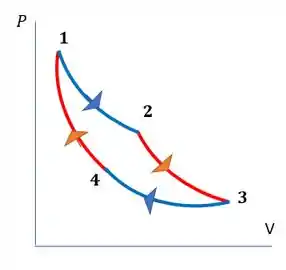
Durante 1 → 2 temos uma expansão isotérmica onde há absorção de calor, 2 → 3 é uma expansão adiabática, 3 → 4 é uma compressão isotérmica onde há liberação de calor e 4 → 1 é uma compressão adiabática.
Se precisamos de um diagrama SV, vamos analisar como o volume e a temperatura podem se relacionar com a entropia. Sabemos da relação:
Ela relaciona uma variação de entropia com uma troca de calor .
As primeiras conclusões que podemos tirar dessa equação é que se de 1 → 2 o calor é adicionado ao sistema, então a entropia aumenta, assim como o volume.
De 2 → 3 é adiabático, assim não há troca de calor e, ou seja, a entropia é constante, mas o volume ainda aumenta.
No processo de 3 → 4 o calor é liberado (saída de calor), então temos uma diminuição da entropia e do volume.
Para finalizar, de 4 → 1 a entropia é constante, porque não há troca de calor, mas o volume continua diminuindo.
Como o eixo vertical do gráfico é a entropia, em e , onde ela é constante, nosso diagrama vai ter segmentos de retas horizontais.
Passo 2
Já sabemos como as variáveis se relacionam, agora precisamos usar outros artifícios para saber como elas vão se comportar nos dois intervalos que não são adiabáticos e a entropia não é constante. A gente quer saber então como se relaciona com nos processos isotérmicos.
No caso da expansão isotérmica de 1 → 2:
Chamaremos de 1 essa temperatura, já que ela se mantém constante. Aí imagina que no começo do processo temos um volume e ao longo do processo temos um volume . Para processos isotérmicos, a variação da entropia é dada por essa fórmula:
Então para saber a variação de entropia em um ponto onde , sendo uma quantidade qualquer de volume dentro do intervalo onde o processo ocorre, teremos:
A gente pode reescrever essa variação de entropia como
Sendo a entropia para , e a entropia para . Substituindo na nossa expressão da variação de entropia:
Agora se a gente isolar teremos uma expressão para em função de :
Passo 3
Bom, no passo 2 achamos uma relação entre e . Podemos pensar que essa é nossa função que descreve o gráfico SV nos intervalos onde temos processos isotérmicos.
Agora precisamos saber como essa função se comporta no gráfico. Para idealizarmos isso podemos fazer a primeira e a segunda derivada da equação anterior, porque elas fornecem a inclinação e a concavidade do caminho. Vamos relembrar como?
Se a gente tem uma função , se a derivada for positiva, nossa função é crescente. Quanto maior , mais rápido essa função cresce. Se a derivada for negativa, a função decresce.
E a segunda derivada? Se , a função é concava para cima, caso contrário, ela concava para baixo.
Então vamos derivar nossa função, assumindo que se trata de um gás ideal e que é constante:
Lembrando que a nossa variável é o volume , o resto é constante
E o que concluímos disso tudo?
Ao longo do caminho 1 →2, a inclinação () do caminho é positiva e à medida que V aumenta a inclinação diminui. Já a concavidade () do caminho é negativa para todos os valores de V.
Passo 4
Podemos fazer a mesma análise para 3 → 4, que é uma compressão:
E ao longo do caminho 3→4, a inclinação () do caminho é positiva e a medida que V diminui a inclinação aumenta. Já a concavidade () do caminho é negativa para todos os valores de V.
Passo 5
Agora comparando esses dois caminhos adiabáticos pelo diagrama PV
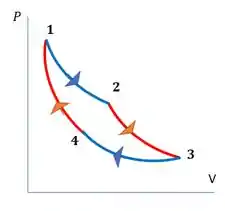
Percebe que o intervalo 1-2 está mais para a esquerda? Isso quer dizer que o volume atinge menores valores nesse intervalo do que os valores que ele atinge no intervalo 4-3. Aí olhando para as derivadas das nossas funções :
Vemos que para o intervalo 1-2 vai ser maior do que para 3-4, porque os valores para esse intervalo são menores. Assim, a inclinação do intervalo 1-2 vai ser maior (a função vai crescer mais rápido)
Quaseee acabamos!
Passo 6
Vamos finalizar desenhando o diagrama SV com todas as características que a gente viu para cada intervalo
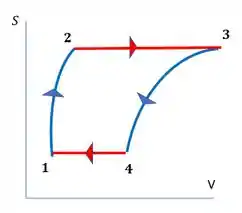
Aí repara que em 1-2 e 2-3 temos de fato uma expansão (o volume aumenta seguindo o sentido da setinha) e em 3-4 e 4-1 temos uma compressão. Isso é uma dica que nosso diagrama está certinho 😊
Resposta
