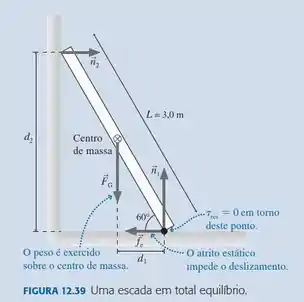
| Uma escada de de comprimento, mostrada na , inclina-se contra uma parede sem atrito. O coeficiente de atrito estático entre a escada e o piso é de . Qual é o mínimo valor de ângulo que a escada pode fazer com a parede sem escorregar?
Passo 1
Um desenho para o problema é:
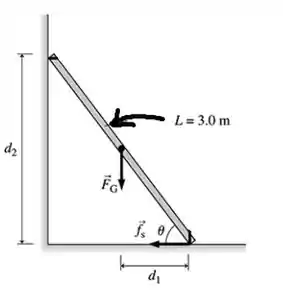
Sendo a força peso e a força de atrito.
Passo 2
Qual é o mínimo valor de ângulo que a escada pode fazer com a parede sem escorregar?
Sabemos que:
E para que não ocorra escorregamento o torque tem que ser zero
Então fazendo o torque como , teremos a força de atrito na horizontal e a força peso na vertical, fica:
Lembre-se que