Determine o momento de inércia da área sombreada em relação ao eixo

Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.
Basicamente precisamos encontrar o momento de inercia em relação ao eixo
Primeiro iremos começar com o diagrama de corpo livre mostrando o elemento diferencial da área sombreada
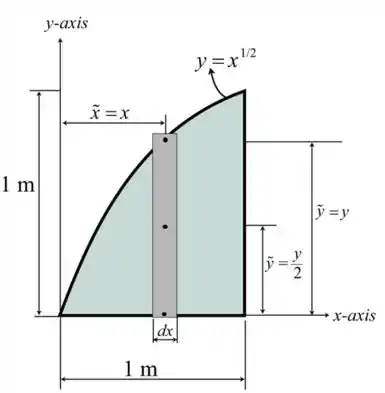
A curva é:
Limites de integração de até
Passo 2
Vamos integrar horizontalmente, usando uma faixa horizontal de altura , com comprimento :
Como o de cada faixa é , então: