Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 8

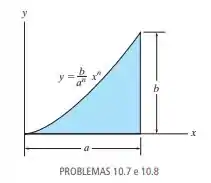
Determine o momento de inércia da área sombreada em relação ao eixo  y .

Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

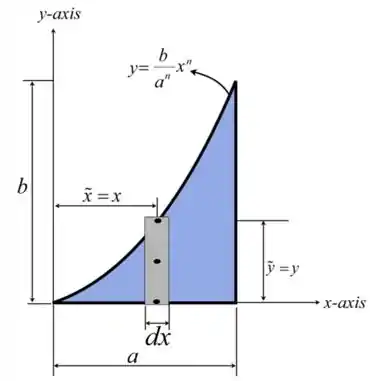
Vamos começar pelo D.C.L mostrando o elemento diferencial da área sombreada.

Passo 2

Escreva a equação da área sombreada.

y = b a n x n             ( 1 )

x = a b 1 n y 1 n

Considere um elemento diferencial retangular em relação ao eixo x   d x com uma espessura e intercepta o limite em ( x , y ) .

Expressaremos a área do elemento diferencial paralelo ao eixo y

d A = y d x

Substituindo (1) para y.

d A = b a n x n   d x

Passo 3

Vamos calcular o momento de inércia da área sombreada em torno do eixo y.

I y = ∫ A x 2 d A

Vamos substituir em Da

I y = ∫ 0 a x 2 b a n x n   d x

Vamos integrar em relação ao eixo x

I y = ∫ 0 a b a n x n + 2 d x

= b a n 1 n + 3 x n + 3 0 a

I y = a 3 b n + 3

Portanto, o momento de inércia da área sombreada em torno do eixo y é de       a 3 b n + 3  

Resposta

I y = a 3 b n + 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma chapa de aço de 800g tem a forma do triângulo isósceles mostrado na FIGURA P12.53. Quais são as coordenadas x e y do centro de massa?Sugestão: divida o triângulo em tiras verticais de largura d x
O momento de inércia de uma haste homogênea em torno de um eixo que passa por seu centro é 1 12 m L 2 . O momento de inércia em torno de um eixo que passa pela extremidade da haste é 1 3 m L 2 . Expli
O professor põe em sua mão duas esferas. Elas possuem a mesma massa, o mesmo raio e a mesma superfície exterior. O professor, então, afirma que uma das esferas é maciça e a outra, oca. Você pode deter
Você dispõe de duas esferas de aço. A esfera2 tem raio duas vezes maior do que o da esfera 1 . Por qual fator o momento de inércia I 2 da esfera 2 excede o momento de inérciaI 1 da esfera 1 ?
Uma furadeira de alta velocidade atinge 2000r p m em 0,50s .a. Qual á a aceleração angular da furadeira?b. Quantas rotações ela completa durante este 0,50s iniciais?