Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 34

Uma escada homogênea, de comprimento L e massa m , está apoiada contra uma parede vertical sem atrito, formando um ângulo de 60 ° com a horizontal. O coeficiente de atrito estático entre a escada e o piso é 0.45 . Se sua massa é quatro vezes a massa da escada, até que altura você pode subir antes que a escada comece a escorregar?

Passo 1

Olha aí! Fiz a representação do diagrama das forças aí embaixo:

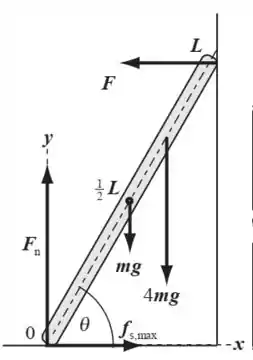
Como a escada tá em equilíbrio, a gente pode fazer equilíbrio das forças e do momento! Bora lá então!

Passo 2

Na vertical a resultante é nula:

F n = m g + 4 m g

F n = 5 m g

Na horizontal a resultante também é nula:

F = F a t

F = μ F n

F = 5 μ m g

Agora vamos fazer momento em relação ao ponto de contato com o chão:

m g c o s θ L 2 + 4 m g c o s θ l = F s e n θ L

Passo 3

Vamos desenvolver essa equação aí de cima, pra isolar l :

m g c o s θ L 2 + 4 m g c o s θ l = ( 5 μ m g ) s e n θ L

4 l c o s θ = 5 μ s e n θ - c o s θ 2 L

l = 5 μ t g θ 4 - 1 8 L

Substituindo valores:

l = 5 0.45 t g 60 ° 4 - 1 8 L

l = 0.85 L

Então, a gente pode subir na escada até 85 % do comprimento dela.

Resposta

É possível subir 85 % da escada até ela começar a deslizar.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco retangular alto e uniforme fica em um plano inclinado, conforme mostrado na Figura 12-45. Um cabo é preso ao topo do bloco para evitar que ele caia no declive. Qual é o ângulo máximo θ para o
Para o cilindro do problema 25, determine uma expressão para a magnitude mínima da força horizontal F → que fará o cilindro rolar sobre o degrau, supondo que ele não deslize na borda.
Uma escada, de massa m e comprimento L , está apoiada contra uma parede sem atrito, formando um ângulo θ com a horizontal. O centro de massa da escada está a uma altura h acima do piso. Uma força F ,
Um homem de 900 N está sentado no topo de uma escada de massa desprezível, colocada sobre um piso sem atrito, como na figura 12-43. Existe um tirante, no meio da escada. O ângulo de abertura é θ = 30