Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 39
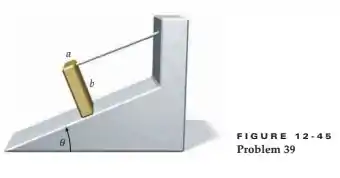
Um bloco retangular alto e uniforme fica em um plano inclinado, conforme mostrado na Figura 12-45. Um cabo é preso ao topo do bloco para evitar que ele caia no declive. Qual é o ângulo máximo θ para o qual o bloco não deslizará na inclinação? Suponha que o bloco tenha uma relação altura-largura, b / a, de 4,0 e o coeficiente de atrito estático entre ele e a inclinação seja μs = 0,80.
Passo 1
Faala ae, beleza??
Então, pelo enunciado, temos que determinar o ângulo da rampa de modo que o bloco fique em equilíbrio, ou seja, queremos que:
E
Beleza, mas pensa aqui comigo: imagina o que acontece quando aumenta além de .
Como a parte superior do bloco é fixada pela corda, o bloco vai girar com apenas a borda direita inferior do bloco permanecendo em contato com o plano. Como vamos ver nessa próxima imagem:
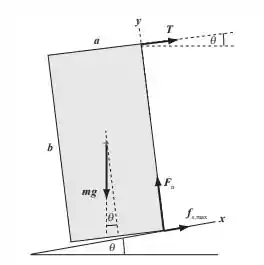
Dessa forma, para que o bloco permaneça em equilíbro nessa situação, imediatamente antes desse escorregamento, e agem na borda direita inferior do bloco. Repare, então, que estamos falando do atrito estático máximo! Por isso podemos usar essa fórmula.
Beleza, então, vamos escolher um sistema de coordenadas em que a inclinação seja a direção +x e a direção de seja a direção +y. Como o bloco está em equilíbrio, podemos aplicar as condições de equilíbrio translacional e rotacional que falamos ali em cima.
Mãos à obra!!
Passo 2
Vamos primeiro garantir que . No eixo , temos:
Como
Agora para o eixo :
Opa, podemos substituir isso na primeira equação de equilíbrio já:
Colocando em evidência:
Passo 3
Show! Agora, olhando para a última condição de equilíbrio:
Beleza, para entender melhor as distâncias ao eixo de rotação, dá uma olhada nessa imagem aqui:
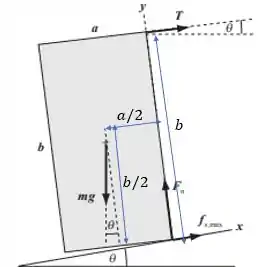
Vamos usar esse ponto inferior do bloco como eixo de rotação, beleza?? Lembrando que temos que olhar para a regra da mão direita também, para saber os sentidos dos torques:
Então, teremos:
Mas no passoa anterior, descobrimos uma expressão para !! Vamos usar aqui:
Podemos usar a relação do enunciado também, que . Então, bora substituir isso e fazer as continhas para achar :
Podemos colocar em evidência:
Onde :
Assim:
Prontinho!! Acabou! 😊