Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 36

Um homem de 900 N está sentado no topo de uma escada de massa desprezível, colocada sobre um piso sem atrito, como na figura 12-43. Existe um tirante, no meio da escada. O ângulo de abertura é θ = 30 ° . (a) Qual é a força exercida pelo piso sobre cada perna da escada? (b) Qual é a tração sobre o tirante? (c) Se o tirante é deslocado para baixo (mantendo-se o mesmo ângulo θ ), a tração sobre ele será a mesma, maior, ou menor do que quando estava na posição mais alta? Explique sua resposta.

Passo 1

Dá uma olhada aí: separei uma das pernas da escada pra mostrar as forças que atuam nela.

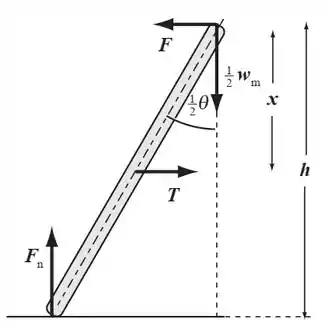
Repara que cada uma vai sustentar metade do peso do homem, pela simetria do problema! Isso já é a resposta da letra (a)!

Passo 2

  1. Cada perna vai sustentar metade do peso, ou seja:

    2. F n = 900 N 2 = 450 N

    Passo 3

  2. Agora, como a escada está em equilíbrio, vamos usar que a soma dos momentos é nula.

    3. ∑ τ = 0

    F n s e n θ 2 D 2 = T s e n θ 2 x

    T = F n D 2 x

    Vamos relacionar D com a altura h usando trigonometria:

    t g θ 2 = D 2 h → D = 2 h t g θ 2

    Como vimos na letra (a), F n = P 2 . Então, substituindo, vamos obter:

    T = P 2 2 h t g θ 2 2 x

    T = P h t g θ 2 2 x   ( * )

    Substituindo valores numéricos:

    T = 900 4.0 t g 15 ° 2 2.0 m

    T = 240 N  

    Passo 4

  3. Olha a equação marcada com ( * ) . Tá vendo que a tração é inversamente proporcional à distância x ? Então se o tirante abaixa, x aumenta e T diminui!

Resposta

  1. F n = 450 N
  2. T = 240 N
  3. A tração diminui.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um lápis sextavado é colocado sobre um caderno (Figura 12-53). Determine o menor coeficiente de atrito, tal que, se a capa do caderno for erguida, o lápis rolará para baixo sem escorregar.
Um a caixa de 8,0 kg, de massa específica uniforme e duas vezes mais alta do que larga, é colocado sobre o piso de um caminhão. Qual é o maior coeficiente de atrito estático entre a caixa e o piso, ta
Um cubo está apoiado em uma parede sem atrito, formando um ângulo θ com o chão, como mostrado na Figura 12-55. Determine o menor coeficiente de atrito estático entre o cubo e o chão, necessário para e
A Figura 12-57 mostra uma escada de 20,0 kg apoiada em uma parede sem atrito e sobre uma superfície horizontal sem atrito. Para evitar que a escada escorregue, sua base é amarrada à parede com um aram
Uma escada homogênea está apoiada contra uma parede vertical sem atrito. O coeficiente de atrito estático entre a escada e o piso é 0,30 . Qual é o menor ângulo entre a escada e a horizontal para que