Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 29

Em um acapamento, você amarra seu barco na extremidade de um cais em um rio que corre, rapidamente, para a direita. O barco está amarrado com uma corrente de 5,0 m de comprimento, como mostrado na figura 12-40. Um peso de 100 N é suspenso no centro da corrente. Com isto, a tração na corrente irá variar, enquanto variar a força da corredeira que afasta o barco do cais, para a direita. A força de arraste da água sobre o barco depende da rapidez da água. Você decide aplicar os princípios de estática que aprendeu nas aulas da física. (Ignore o peso da corrente.) A força de arraste sobre o barco é de 50 N . (a) Qual é a tração na corrente? (b) Qual é a distância do barco ao cais? (c) A maior tração que a corrente pode suportar é de 500 N . Qual é a menor força de arraste sobre o barco capaz de romper a corrente?

Passo 1

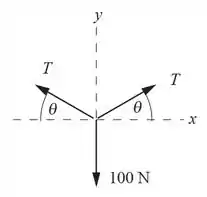
Se liga! Nas cordas que ligam o barco ao cais, com o peso, as forças ficam distribuídas assim:

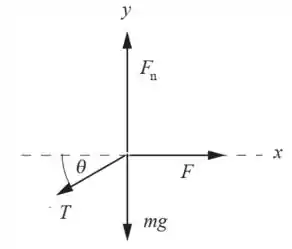
E no barco, as forças ficam assim, distribuídas em força vertical, tração, peso e a força de arrasto:

Os dois estão em equilíbrio estático, então podemos fazer equilíbrio de momentos e equilíbrio de forças!

Passo 2

  1. Para o barco, na horizontal:

    2. F = T c o s θ

    E para o peso:

    2 T s e n θ = 100

    Dividindo as duas expressões, vamos obter:

    2 T s e n θ T c o s θ = 100 F

    t g θ = 50 F

    θ = a r c t g 50 F

    A força é de 50 N , então:

    θ = a r c t g 50 50 = a r c t g 1

    θ = 45 °

    Então a gente pode achar a tração!

    2 T s e n 45 ° = 100

    T = 71 N

    Passo 3

  2. Agora vamos relacionar a distância do bote com o tamanho do fio! Olhando pro desenho você vê que é pelo cosseno do ângulo!

    3. c o s θ = d 2 L 2 = d L

    d = L c o s θ

    Substituindo:

    d = 5 c o s 45 °

    d = 3.5 m

    Passo 4

  3. A resultante vertical e a força do arrasto somadas (vetorialmente) são o que gera tração na corda. Pelo Pitágoras nas forças, usando 500 N na força da corrente, que é o máximo que ela aguenta:

F v 2 + F 2 = 500 2

F = 500 2 - 50 2

F = 497 N ≅ 0.5 k N

Resposta

  1. T = 71 N
  2. d = 3.5 m
  3. F = 0.5 k N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O sistema da figura ao lado está em equilíbrio. Um bloco de concreto com uma massa de 225k g está pendurado na extremidade de uma longarina com uma massa de 45,0k g . Para os ângulos ϕ=30,0º º e θ=45,
Na figura, a extremidade de uma viga homogênea de 222N de peso está presa por uma dobradiça a uma parede. A outra extremidade é sustentada por um fio que faz o mesmo ângulo θ = 30 ° com a viga e com a
Uma alpinista com 533,8 N de peso é sustentada por uma corda de segurança presa a um grampo em uma das extremidades e a um mosquetão na cintura da moça na outra extremidade. A linha de açaí da força e
Na figura, um bloco de 15k g é mantido em repouso através de um sistema de polias. O braço da pessoa está na vertical; o antebraço faz um ângulo θ = 30 ° com a horizontal. O antebraço e a mão têm uma
Na figura, suponha que o comprimento L da barra uniforme seja 3,00m e seu peso seja 200N . Suponha ainda que o bloco tenha um peso P=300N e que θ=30,0 ° . O fio pode suportar uma tensão máxima de 500N