Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.9 - Ex. 55

Uma esfera não condutora de raio R = 5,60   c m possui uma distribuição de cargas não uniforme ρ = 14,1 p C m 3 r R   , onde r é a distância do centro da esfera. (a) Determine a carga da esfera. Determine o módulo E do campo elétrico (b) em r = 0 ; (c) em r = R / 2,00 ; (d) em r = R   (e) Faça um gráfico de E em função de r .

Passo 1

Galerinhaa de peão, vamos começar mais umaa !!

Nesse problema temos uma esfera não condutora com raio R = 5,60   c m e com densidade de cargas ρ = 14,1 p C m 3 r R . Nosso objetivo é obter o campo elétrico E em r = 0 , r = R / 2 e em r = R . Também precisamos obter a carga da esfera que gera este campo.

A primeira coisa a se fazer, é encontrar a expressão para a carga total dessa esfera, ok?

Mas antes nós vamos obter a carga para um raio r qualquer, vamos ver?

q i n t = ∫ d Q = ∫ ∫ ∫ ρ d V

Se escolhermos uma esfera oca com espessura  d r  como  d V  nós temos:

d V = 4 π r 2 d r

q i n t = ∫ ρ d V

= 4 π ∫ 0 r 4 π r ² ρ d r

Sacou? Bora começar! 😁

Passo 2

Lembrando que:

ρ   =   14,1 ∙ 10 - 12 C m 3 r R

Então:

q i n t = 4 π 14,1 ∙ 10 - 12 R ∫ 0 r r 3 . d r

= 4 π 14,1 ∙ 10 - 12 R r 4 4

= 14,1 ∙ 10 - 12 π r 4 R

Belezaa !! Achamos a carga dentro dessa esfera com relação a distância do centro a qual estamos avaliando, r , e o raio total, R .

Isso já nos permite resolver a letra (a), como queremos a carga total vamos simplesmente substituir r = R , na fórmula que acabamos de achar:

q i n t = 14,1 ∙ 10 - 12 π R 4 R = 14,1 ∙ 10 - 12 π R 3

Sabendo que R   =   0,056   m :

q i n t = 14,1 × 10 - 12 π 0,056   m 3

q i n t = 7,78 ∙ 10 - 15   C

Passo 3

De agora em diante queremos o campo elétrico, então vamos colocar a fórmula que achamos da carga interna dentro da fórmula para o campo elétrico quando r ≤ R , ok?

E = 1 4 π ε 0 . q i n t r 2

= 1 4 π ε 0 . 14,1 ∙ 10 - 12 π r 4 R r 2

E = 3,525 ∙ 10 - 12 r 2 R ε 0

Agora já praticamente resolvemos o dilema !!

Tranquilo até aqui? 😬

Passo 4

Na letra (b) temos r = 0 , então basta substituirmos:

E = 3,525 ∙ 10 - 12 r 2 R ε 0 = 0 N C

Passo 5

Na letra (c) temos r   = R 2 , então basta substituirmos:

E = 3,525 ∙ 10 - 12 R 2 2 R ε 0

= 3,525 ∙ 10 - 12 R 4 ε 0

E = 3,525 ∙ 10 - 12 0,056   m 4 8.85 ∙ 10 - 12   C 2 N m 2

E = 5,58 ∙ 10 - 3 N C

Agora na letra (e) nós temos r   =   R :

E = 3,525 ∙ 10 - 12 R 2 R ε 0 = 3,525 ∙ 10 - 12 R ε 0

E = 3,525 ∙ 10 - 12 0,056   m 8.85 ∙ 10 - 12   C 2 N m 2

E = 2,23 ∙ 10 - 2 N C

Bacana, não é? 😉

Passo 6

Para finalizar a questão nós precisamos montar um gráfico de E × r , e para isso vamos olhar novamente a equação que obtemos:

E = 3,525 ∙ 10 - 12 r 2 R ε 0

Substitituindo R e ε 0 :

E = 3,525 ∙ 10 - 12 r 2 0,056 8.85 ∙ 10 - 12 = 7,11 r 2

Então até r = R nós temos um curva, onde o campo elétrico vai aumentando junto com o raio!! E quando r > R nós teremos uma diminuição deste campo, já que E ∝ 1 r 2 !

Vamos ver?

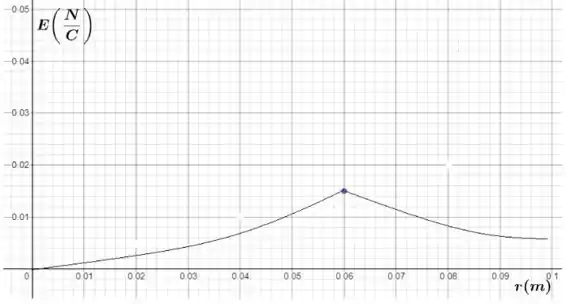
E chegamos ao fim de mais uma questão toop!! O que achou? Responde Aí! 😊

Resposta

( a ) 7,78 × 10 - 15 C  

(b) 0

(c) 5,58 m N C

(d)   22,3 m N C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma casca esférica tem raio interno R i n t e raio externo R e x t . A casca contém carga total Q, uniformemente distribuída. O interior da casca não contém carga nem matéria.a. Determine o campo elét
Todos os exemplos da lei de Gauss usaram superfícies altamente simétricas através das quais a integral de fluxo é nula ou igual a E A . Nós também alegamos que o fluxo resultante Φ e = Q i n t ε 0 é i
Um cilindro infinito longo e de raio R apresenta uma densidade linear de carga λ . A densidade volumétrica de carga (em C / m 3 ) no interior do cilindro ( r ≤ R ) é dada por ρ r = r ρ 0 / R , onde p
A intensidade do campo elétrico a 2,0c m da superfície de uma esfera metálica com 10c m de diâmetro é de 50.000N C . Qual é a carga (em n C ) da esfera?
Explique por que a simetria da figura 25 - 16 nos restringe a consideração que E só tem componentes perpendiculares a chapa? Por que o exemplo, E não poderia ter componentes paralelos à chapa ?