Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 28.Exercícios e Problemas - Ex. 53

Uma casca esférica tem raio interno R i n t e raio externo R e x t . A casca contém carga total Q, uniformemente distribuída. O interior da casca não contém carga nem matéria.

a. Determine o campo elétrico fora da casca, r ≥ R e x t .

b. Determine o campo elétrico no interior da casca, r ≤ R i n t .

c. Determine o campo elétrico dentro da casca, R i n t ≤ r ≤ R e x t .

d. Mostre que suas soluções ajustam-se umas às outras nas bordas interna e externa da casca. e. Desenhe o gráfico de E versus r.

Passo 1

Faaala galera, para o item (a), basta utilizar a lei de Gauss

E A = Q ε 0

E = Q ε 0 A

Para a área de uma esfera, temos

E = Q ε 0 4 π r 2

Com r ≥ R

E = Q ε 0 4 π 1 r 2 r ^

Passo 2

Como o campo elétrico depende da carga, e o enunciado nos diz que não há carga. Logo

r ≤ R i n t

E = 0

Passo 3

E A = Q ε 0

Vamos delimitar o r para este espaço dentro da casca

A densidade de carga volumétrica é

D = Q V

Substituindo a carga

E A = D V ε 0

Agora vamos substituir o volume dentro da casca

E 4 π r 2 = D 4 / 3 π r 3 - R i n t 3 ε 0

A densidade volumétrica em termos de carga

E 4 π r 2 = Q 4 / 3 π r 3 - R i n t 3 ε 0 4 / 3 π R e x t 3 - R i n t 3

E podemos simplificar

E 4 π r 2 = Q r 3 - R i n t 3 ε 0 R e x t 3 - R i n t 3

E = Q r 3 - R i n t 3 4 π r 2 ε 0 R e x t 3 - R i n t 3

E = Q 4 π r 2 ε 0 ⋅ r 3 - R i n t 3 R e x t 3 - R i n t 3

Por fim :)

E = 1 4 π ε 0 ⋅ Q r 2 ⋅ r 3 - R i n t 3 R e x t 3 - R i n t 3 r ^

Passo 4

Olhando a equação obtida no passo anterior

E = 1 4 π ε 0 ⋅ Q r 2 ⋅ r 3 - R i n t 3 R e x t 3 - R i n t 3 r ^

Caso igualássemos r = R i n t , então E = 0

E para r = R e x t

E = 1 4 π ε 0 ⋅ Q R e x t 2 ⋅ R e x t 3 - R i n t 3 R e x t 3 - R i n t 3 r ^

E = 1 4 π ε 0 ⋅ Q R e x t 2 r ^

Logo, nossos resultados são coerentes com os passos anteriores

Passo 5

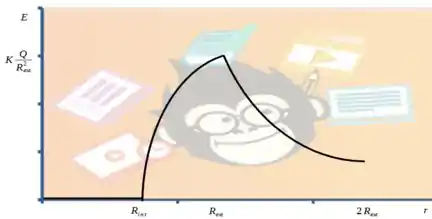
Sabemos que enquanto r ≤ R i n t o campo elétrico é zero. A partir daí ele vai subindo até atingir um máximo quando está em R e x t e depois vai se distanciando da carga e diminuindo seu campo elétrico de acordo com a equação do Passo 3

Resposta

a

E = Q ε 0 4 π 1 r 2 r ^

b.

E = 0

c.

E = 1 4 π ε 0 ⋅ Q r 2 ⋅ r 3 - R i n t 3 R e x t 3 - R i n t 3 r ^

d. Demonstração no Passo 4

e. (Passo 5)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera maciça, não condutora, de raio R , tem uma distribuição de carga não uniforme de densidade volumétrica dada por ρ = ρ 1 r R , onde ρ 1 é uma constante e r é a distancia ao centro da esfera.
A Fig. 25-40 mostra uma carga puntiforme q = 1,0 × 10 - 7C , no centro de uma cavidade esférica de raio 3,0c m existente numa peça de metal. Use a lei de Gauss para determinar o campo elétrico (a) no
Uma casca esférica, fina e descarregada, tem uma carga puntiforme q no centro. Deduza expressões para o campo elétrico (a) no interior da casca e (b) fora da casca, usando a lei de Gauss. (c) A casca
Uma esfera não-condutora tem uma densidade volumétrica de carga ρ . Seja r o vetor que vai do centro da esfera até um ponto genérico P dentro da esfera. (a) Mostre que o campo elétrico em P é dado por
Uma casca fina esférica metálica de raio a tem uma carga q a . Concêntrica com ela está uma outra casca fina, esférica, metálica de raio b (onde ba ) e carga q b . Determine o campo elétrico em pontos