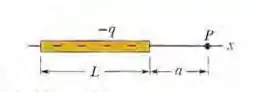
Na Fig. 22-46, uma barra não condutora de comprimento tem uma carga uniformemente distribuída. (a) Qual é a densidade linear de cargas da barra? Determine (b) o módulo e (c) a direção (em relação ao semieixo positivo) do campo elétrico produzido no ponto , situado no eixo , a uma distância da extremidade da barra. Determine o módulo do campo elétrico produzido em um ponto situado no eixo , a uma distância do centro da barra, (d) pela barra e (e) por uma partícula de carga colocada no lugar anteriormente ocupado pelo centro da barra.

Item (a)

Como a carga está uniformemente distribuída na barra, a densidade linear nada mais é do que a divisão da carga pelo tamanho total da barra :

Substituindo os valores e :

Tranquilo até aqui? 😊

Item (b)

Vamos posicionar o eixo na extremidade esquerda da barra e o sentido crescente para a direita conforme a figura abaixo:

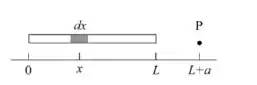
Chamaremos de um segmento infinitesimal da barra como mostra a figura acima, então como a carga é uniformemente distribuída, podemos relacionar a densidade linear de carga com esse segmento fazendo:

E como a distância está no deixo , podemos escrever:

E assim, ficamos com...

Sendo que pode ser considerada uma carga pontual. O campo elétrico gerado por uma carga pontual é igual a:

Onde: é uma constante (, é a carga da partícula que gera o campo elétrico e é a distância entre o ponto onde desejamos calcular o campo elétrico e a carga que o gera.

Como o ponto encontra-se no eixo da barra, o vetor campo elétrico tem apenas componente , que pode ser dada como, para cada ponto da barra:

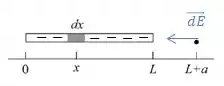
Ou seja, cada pedacinho da barra gera uma componente ! Show, mas observe que a distância entre esse pedaço e o ponto P é dado pela diferença:

Está acompanhando? 😁

Entendeu tudo? Então para calcular o campo em toda a barra, devemos integrar em x:

Vamos passar tudo que não depende de para fora da integral:

Para resolver essa integral, vamos fazer uma substituição simples:

Fazendo a substituição...

Resolvendo...

Aplicando os limites de integração...

Substituindo , , e a permissividade do vácuo .

Vamos fazer as multiplicações:

Fazendo as novas multiplicações:

Por fim nos resta:

E como vimos, o campo elétrico vai ser dado apenas por essa componente horizontal:

O que indica que o módulo do campo elétrico é .

Estamos quase lá! 😎

Item (c)

Como nossa carga é negativa, as linhas de campo elétrico sempre irão apontar para ela, logo o sinal negativo no indica que o campo elétrico aponta no sentido negativo do eixo , isto é, do semieixo positivo, ou seja, aponta para a barra!

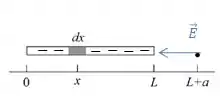
Bora continuar! 😐

Item (d)

Como a distância entre o ponto onde desejamos calcular o campo é muito mais distante do que o tamanho da barra:

Podemos usar a aproximação:

Assim a barra se comporta como uma carga pontual, como podemos ver no desenho, a distância é tão grande, que o tamanho da barra já não interfere

Ou seja, o campo se torna o campo de uma partícula pontual:

Onde vamos substituir a distância por apenas :

Vamos então substituir os valores que são dados: , e .

Assim,

E finalmente...

Item (e)

Note que a expressão que obtemos na aproximação do item anterior é o mesmo de uma partícula de carga situada a uma distância do ponto , assim, o resultado é o mesmo do item anterior

E aí! entendeu tudo? Responde Aí! 😉