Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 4.Problemas - Ex. 2b

Uma esfera está uniformemente carregada, com carga total q . Tomando q = - e , com carga puntiforme + e no centro da esfera como modelo para o átomo de hidrogênio, qual é a expressão do potencial?

Passo 1

Se liga! Vamos começar pensando pela parte externa, na regão onde R ≤ r ≤ ∞ .

Como a carga da esfera é - e , ao colocarmos uma carga puntiforme no centro da esfera de intensidade + e teremos uma situação onde todas as cargas da esfera estarão no centro.Sendo assim, ao fazermos a soma das cargas dentro da esfera encontraremos um resultado igua a zero. Portanto

V r = 0 .

Passo 2

Agora vamos considerar que no infinito o potencial é zero, sendo assim

V r - V ∞ = V r = ∫ ∞ R q 4 π ϵ 0 r 2 d r = q 4 π ϵ 0 R  

Passo 3

Para a parte interna podemos começaremos admitindo que o campo produzido pela carga puntiforme positiva é

E + = e 4 π ϵ 0 r 2

Como a carga é positiva, o campo aponta para fora na direção radial

E + → = e 4 π ϵ 0 r 2   r ^

Como a carga negativa está distribuída na esfera, precisaremos aplicar a lei de Gauss

ϕ s = ∮ E d A = q i n t ϵ 0

Se liga na figura!

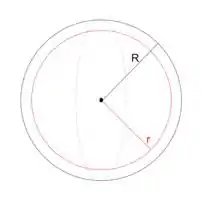
Neste caso devemos usar a área da superfície gaussiana

A = 4 π r 2

E a carga será a que está contida dentro da gaussiana

q i n t = - e r 3 R 3

Isso nos da que

E - = - e 4 π ϵ 0 r 2 r 3 R 3

Como a carga é negativa, o campo aponta para dentro na direção radial

E - → = - e 4 π ϵ 0 r 2 r R 3   r ^

Passo 4

Agora vamos calcular o potencial, lembrando que fora o potencial é zero.

V r - V R = V r = ∫ R r e 4 π ϵ 0 r 2 d r + ∫ R r - e 4 π ϵ 0 r 2 r 3 R 3 d r

= e 4 π ϵ 0 1 r - 1 R + e 4 π ϵ 0 R 3 r 2 2 - R 2 2

= e 4 π ϵ 0   1 r - 1 R + r 2 2 R 3 - 1 2 R

= e 4 π ϵ 0 1 r - 1 R r 2 2 R 2 - 3 2

Resposta

V ( r ) = e 4 π ϵ 0 1 r - 1 R r 2 2 R 2 - 3 2 D e n t r o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Problemas de 73 a 75 é fornecida uma equação para ser usada na resolução de um problema. Para cada uma delas:a. Redija um problema realista para o qual essa a equação seja correta.b. Obtenha a sol
As esferas da FIGURA PD29.79, com 2,0 mm de diâmetro, partem do repouso. Quais serão as velocidades vC e vD no instante em que elas colidem?
As esferas da FIGURA PD29.78, com 2,0 mm de diâmetro, partem do repouso. Quais serão as velocidades vA e vB quando as esferas estiverem muito afastadas?
Um elétron parte do repouso em x = 2 m em presença do potencial representado na FIGURA Q30.5 Ele se moverá? Em caso afirmativo, para o lado esquerdo ou para o direito? Explique.
Quanto trabalho a escada rolante de cargas realiza para transferir 1,0 u C de carga do terminal negativo para o terminal positivo de uma bateria de 1,5 V?