Uma esfera de vidro de raio tem um índice de refração de . Um peso de papel de altura é frabricado cortando a esfera ao longo de um plano situado a centro da esfera. O peso de papel é colocado sobre uma mesa e visto de cima por um observador situado a uma distância da superfície da mesa (Fig. 34-38). Quando vista através do peso de papel, a que distancia a superfície da mesa parece estar do observador?
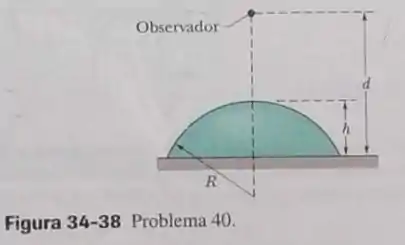
Passo 1
Bom, pelos valores que foram dados e pelo tipo de problema, sabemos que vamos precisar da equação de superfícies refratoras esféricas:
Passo 2
Como a mesa q é o objeto, ela está a uma distância de valor de onde o observador olha, então , e como o primeiro meio é o ar, , os outros valores foram dados pelo enunciado, vamos então isolar :
E substituir cada valor:
Passo 3
Agora que a gente tem o valor de basta somarmos esse valor à distância do observador até a superfície que chamaremos de . Essa distância é o mesmo que a distância ate a mesa menos a altura da superfície:
E agora somamos só o módulo de , já que a gente precisa da distância da imagem até o observador e o sinal nesse caso é qualitativo e aparece só por causa da convenção que se usa para calcular cada grandeza (a origem fica no ponto onde acontece a mudança de meio, do ar para a esfera):