Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 33.Problemas Adicionais - Ex. 77

Arco-Íris. A figura 33-67 mostra um raio luminoso entrando e saindo de uma gora d’água esférica depois de sofrer uma reflexão interna. A diferença entre a direção final do raio e a direção inicial é o ângulo de desvio θ d e s v . (a) Mostre que θ d e s v é dado por θ d e s v = 180 ° + 2 θ i - 4 θ r em que θ i é o ângulo de incidência do raio na gora e θ r é o ângulo do raio refratado. (b) Use a lei de Snell para expressar θ r em termos de θ i e do índice de refração n da água. Em seguida use uma calculadora gráfica ou um computador para plotar θ d e s v em função de θ i para n = 1,331 (luz vermelha) e para n = 1,333 (luz azul).

A curva da luz vermelha e a curva da luz azul passam por um mínimo para valores diferentes do θ d e s v , o que significa que existe um ângulo de desvio mínimo diferente para cada cor. A luz de uma cor que sai da gora com o ângulo de desvio mínimo é especialmente intensa pois os raios se acumulam na vizinhança desse ângulo. Assm, a luz vermelhamais intensa sai da gota com um ângulo e a luz azul mais intensa sai da gota com outro ângulo.

Determine o ângulo de desvio mínimo ( c ) para a luz vermelha e (d) para a luz azul. (e) Se essas cores estão nas extremidades de um arco-íris, qual é a largura angular do arco-írirs?

Passo 1

a) A primeira contribuição que temos para o desvio total da luz é a primeira refração que pode ser dada por:

∆ θ 1 = θ i - θ r

A segunda contribuição é uma reflexão, desta forma temos que o ângulo entre o raio luminoso antes da reflexão e a normal é θ r o ângulo após a reflexão também é θ r , levando em conta a inversão do sentido da propagação do raio de luz, temos:

∆ θ 2 = 180 ° - 2 θ r

A terceira e última contribuição é a refração que acontece quando o raio sai da gota, que é:

∆ θ 3 = θ i - θ r

Portanto o ângulo de desvio é:

θ d e s v = ∆ θ 1 + ∆ θ 2 + ∆ θ 3 = θ i - θ r + 180 ° - 2 θ r + θ i - θ r

θ d e s v = 180 ° + 2 θ i - 4 θ r

Passo 2

b) Utilizando a lei de Snell para expressar θ r em termos de θ i e do índice de refração n da água:

n a r s e n   θ i = n á g u a s e n θ r

Considerando o índice de refração do ar aproximadamente 1:

θ r = s e n - 1 1 n s e n θ i

Substituindo esse valor de θ r no ângulo de desvio:

θ d e s v = 180 ° + 2 θ i - 4 s e n - 1 1 n s e n θ i

Agora plotando o gráfico do ângulo de desvio em função do ângulo de incidência:

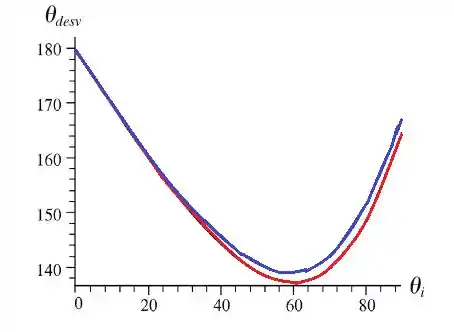
Passo 3

c) Para determinar o θ d e s v mínimo para a luz vermelha temos duas maneiras de fazer. A primeira é utilizando o programa computacional usado para fazer o gráfico e a segunda é derivando a função θ d e s v = 180 ° + 2 θ i - 4 s e n - 1 1 1,331 s e n θ i

e igualando a zero. Aqui vamos utilizar o gráfico. A partir dele encontramos que θ i e θ d e s v mínimo é:

θ i = 59,5 °

θ d e s v = 137,6 °

Passo 4

d) Para determinar o θ d e s v mínimo para a luz azul temos duas maneiras de fazer. A primeira é utilizando o programa computacional usado para fazer o gráfico e a segunda é derivando a função θ d e s v = 180 ° + 2 θ i - 4 s e n - 1 1 1,333 s e n θ i

e igualando a zero. Aqui vamos utilizar o gráfico. A partir dele encontramos que θ i e θ d e s v mínimo é:

θ i = 58,5 °

θ d e s v = 139,4 °

Passo 5

e) A largura angular do arco-íris é dada pela diferença do ângulo de desvio, que é:

139,4 ° - 137,6 ° = 1,7 °

Resposta

b) θ d e s v = 180 ° + 2 θ i - 4 s e n - 1 1 n s e n θ i

c) θ d e s v = 137,6 °

d) θ d e s v = 139,4 °

e) 1,7 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um objeto O está sobre o eixo central de uma superfície refratora esférica. Para cada problema, a Tabela 34-5 mostra o índice de refração n 1 do meio em que se encontra o objeto, ( a ) o índice de ref
Um objeto O está sobre o eixo central de uma superfície refratora esférica. Para cada problema, a Tabela 34-5 mostra o índice de refração n 1 do meio em que se encontra o objeto, ( a ) o índice de ref
Um objeto O está sobre o eixo central de uma superfície refratora esférica. Para cada problema, a Tabela 34-5 mostra o índice de refração n 1 do meio em que se encontra o objeto, ( a ) o índice de ref
Na Fig. 34-37, um feixe de raios luminosos paralelos produzido por um laser incide em uma esfera maciça transparente de índice de refração n . ( a ) Se uma imagem pontual é produzida na superfície pos
Uma esfera de vidro de raio R = 5,0 tem um índice de refração de n = 1,6 . Um peso de papel de altura h = 3,0c m é frabricado cortando a esfera ao longo de um plano situado a 2,0c m centro da esfera.