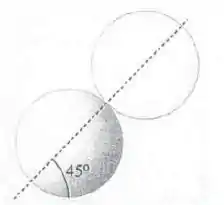
As esferas vistas na Figura 5.18 têm cada uma massa e estão em equilíbrio mecânico. Supondo que não haja atrito entre as bolas, nem entre elas e a caixa, identifique todas as forças atuando sobre as esferas e calcule o seu valor.
Passo 1
Oi pessoas, tudo certo com vocês? Espero que sim 😊. Nessa questão vamos entender mais sobre equilíbrio de corpos.
Primeiro vamos inserir as forças que atuam sobre o bloco. Note que podemos representar assim:
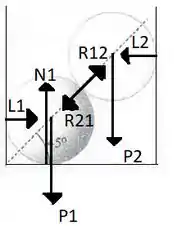
Em que:
: forças das paredes atuando sobre cada bola.
: Peso de cada bola.
: força do fundo da caixa sobre a bola de baixo.
: Força de uma bola sobre a outra.
Passo 2
Certo, agora que já inserimos cada força, vamos calcular. Já sabemos que o peso de cada bola é dada por:
Note que, a soma da força do fundo da caixa sobre a bola () vai ser igual a soma dos pesos de cada bola, ou seja:
Observe também que a força que a parede atua sobre a bola vai ser igual ao seu peso, assim
Podemos notar também que a força de reação de uma bola na outra, se decompormos no eixo x, ela vai ser igual a força que a parece atua sobre a bolas, ou seja