Empurrando ao longo de um piso com velocidade , um bloco segue escorregando por uma distância após a força de empurrão deixar de ser exercida.
- Se a massa do bloco fosse duplicada, e sua velocidade inicial permanecesse a mesma, que distância o bloco percorreria até parar?
- Se a velocidade inicial fosse duplicada para e a massa fosse mantida a mesma, que distância o bloco percorreria até parar?
Passo 1
Inicialmente, devemos perceber que o bloco para devido a força de atrito atuante.
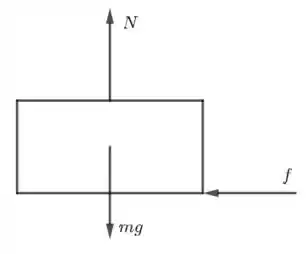
Passo 2
A força de atrito, , pode ser calculada por:
sendo a força normal entre o bloco e a superfície. Para o caso esquematizado na figura, o corpo está em equilíbrio na vertical, de modo que (forças para cima = forças para baixo):
Assim,
Note que a força de atrito depende da massa do corpo. Assim, corpos de um mesmo material, porém com massas diferentes, experimentam forças de atritos diferentes.
Passo 3
Okay. Agora já montamos o diagrama de corpo, de modo que sabemos que atua uma única força no corpo na direção do movimento (eixo x). Tal força é constante, de modo que o movimento é uniformemente acelerado. O cálculo da aceleração pode ser feito utilizando a 2° Lei de Newton.
Passo 4
Podemos, portanto, aplicar a equação de Torricelli:
A velocidade inicial é dada: ; a velocidade final é nula (pois o corpo para); (o sinal negativo ocorre, pois, a força está apontada para o sentido contrário da velocidade). Assim, temos que
Passo 5
- Note que a expressão para não depende da massa. Assim, não importa se a massa do bloco for duplicada, a distância irá continuar valendo .
- Se a velocidade for mudada para , temos:
Portanto, a distância percorrida até o corpo parar será 4 vezes maior.
Observação: note que, embora a força de atrito dependa da massa do corpo, a aceleração não depende da massa. Isso acontece pois, quanto maior m maior será a força de atrito; em contrapartida, maior será a inércia do corpo, de modo que os efeitos se anulam.
Resposta
Ei, a resposta está no passo a passo :)