Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 10.Problemas - Ex. 55

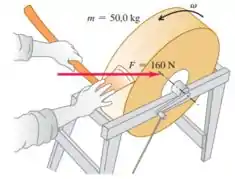
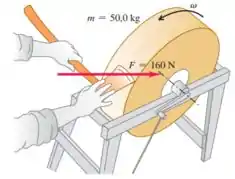
Um esmeril em forma de disco sólido com diâmetro de 0,520 m e massa de 50,0 kg gira a 850 rot/min. Você pressiona um machado contra sua periferia com uma força normal de 160 N (Figura P10.54), e o esmeril atinge o repouso em 7,50 s. Ache o coeficiente de atrito entre o machado e o esmeril. Despreze o atrito nos mancais.

Passo 1

E aiiiiiiiii galera, tudo bom com vocês?

Vamos fazer mais uma questão!!

Bom... o enunciado nos diz que um esmeril em forma de disco sólido com diâmetro de 0,520   m e massa de 50,0   k g gira a 850   r o t / m i n .

Você pressiona um machado contra sua periferia com uma força normal de 160   N , conforme a figura abaixo, e o esmeril atinge o repouso em 7,50   s .

Queremos calcular o coeficiente de atrito entre o machado e o esmeril.

Para isso, precisamos da seguinte expressão:

∑ τ = I α

Onde τ é o torque, I é o momento de inércia e α é a aceleração angular.

Passo 2

A aceleração angular é em termos das velocidades angulares inicial ω i e final ω f da equação:

α = ω f - ω i Δ t

Onde ω i = 850 * 2 π 60 = 85 π 3 .

Substituindo:

α = 0 - 85 π 3  rad.s  7.50 s ∴

α = - 34 π 9 r a d / s 2

Passo 3

O momento de inércia do esmeril (disco sólido) é achado na Tabela 9.2, onde:

I = 1 2 M R 2

Assim, substituindo os valores, temos:

I = 1 2 ( 50.0 k g ) ( 0.260 m ) 2 ∴

I = 1.69   k g m 2

Passo 4

Deixe a direção de rotação do esmeril ser a direção positiva.

A força normal F resulta em uma força de atrito f agindo em uma direção oposta a rotação do esmeril e a magnitude desta força é encontrada com a seguinte equação:

f = μ k F

onde μ k é o coeficiente de atrito cinético que estamos tentando encontrar.

O torque devido a esta força é negativo. Modele o esmeril como um objeto rígido:

∑ τ = - τ f = I α

O torque devido a f 1 é τ f = f R , onde R é o braço de momento da força, uma vez que é exercido no machado a uma distância R do eixo de rotação:

∑ τ = - f R = I a ∴

- μ k F R = I α ∴

μ k = - I α F R

Substituindo os valores, temos:

μ k = - 1.69 k g ⋅ m 2 - 34 π 9 r a d s 2 160 N 0.260 m

μ k = 0.482

Resposta

μ k = 0.482

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Por que a seguinte situação é impossível? Uma viga uniforme de massa m b=3,00k g e comprimento l=1,00m suporta blocos com massas m 1=5,00k g e m 2=15,0k g em duas posições, conforme mostrado na Figura
Nos exercícios de estudos de Fisiologia, às vezes é importante determinar a localização do centro de massa de uma pessoa. Esta determinação pode ser feita com o arranjo mostrado na Figura P10.29. Uma
Considere o sistema mostrado na Figura P10.21 com m 1=20,0k g , m 2=12,5k g , R=0,200m e a massa da roldana M=5,00k g . O corpo m 2 está repousando no chão, e o m 1 está 4,00m acima do chão quando é l
O braço na Figura P10.35 pesa 41,5N . A força gravitacional sobre ele age através do ponto A . Determine os módulos da força de tensão F → t no músculo deltoide e a força F → s exercida pelo ombro no
Uma viga uniforme repousando em dois pinos tem comprimento L=6,00m e massa M=90,0k g . O pino à esquerda exerce uma força normal n 1 sobre a viga, e o outro, localizado a uma distância l=4,00m da extr