Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 21
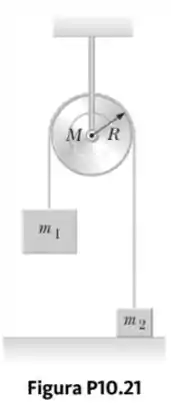
Considere o sistema mostrado na Figura P10.21 com , , e a massa da roldana . O corpo está repousando no chão, e o está acima do chão quando é liberado do repouso. O eixo da roldana não tem atrito. O fio é leve, não estica e não escorrega na roldana.
- Calcule o intervalo de tempo exigido para atingir o chão.
- Como você responderia à variação se a roldana não tivesse massa?
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
Letra a:
Seja a tensão no cabo acima de a tensão na corda acima da massa mais leve. Os dois blocos se movem com a mesma aceleração porque o cabo não estica, e a aceleração angular da polia é . Para a massa mais pesada temos:
Para a massa mais leve:
Assumimos que a polia é um disco uniforme, :
Some as três equações:
Passo 2
Letra b:
Se a polia não tivesse massa, a aceleração seria maior por um fator de 35/32.5 e o tempo mais curto pela raiz quadrada de fator 32.5/35. Ou seja, o tempo seria reduzido em 3,64%.
Resposta
- Se a polia não tivesse massa, a aceleração seria maior por um fator de 35/32.5 e o tempo mais curto pela raiz quadrada de fator 32.5/35. Ou seja, o tempo seria reduzido em 3,64%.