Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 32.1 - Ex. 30

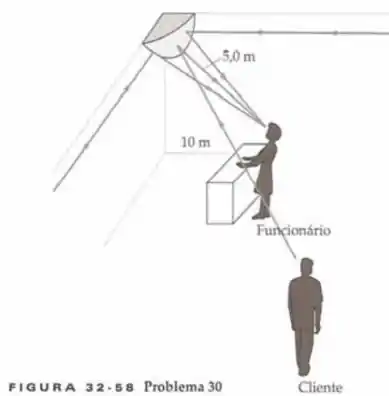
Espelhos convexos são usados em muitas lojas para fornecer um grande ângulo de vigilância em um espelho com tamanho razoável. Seu trabalho de verão é em uma loja de conveniência que usa o espelho mostrado na Figura 32-58. Este arranjo permite que você (ou o funcionário) supervisione a loja interia quando você está a 5,0   m do espelho. O espelho tem raio de curvatura de 1,2   m . Considere que todos os raios sejam paraxiais.

a) Se um cliente está a 10   m do espelho, a que distância do espelho estará a imagem dele?

b) A imagem está na frente ou atrás do espelho?

c) Se o cliente tem 2,0   m de altura, que altura terá a imagem dele?

Passo 1

E aí meus caros! Na paz do nosso senhor Jeová? (amém) Nessa questão podemos usar a equação do espelho e a relação entre o comprimento focal de um espelho e seu raio de curvatura para encontrar a localização da imagem. Podemos então usar a definição da ampliação lateral do espelho para encontrar a altura da imagem formada no espelho. Fechou?

Passo 2

Logo de cara, a letra a) nos pede para determinar a distância imagem! Vamos lá, não há muita enrolação para responde-la! Utilizando-se de Gauss:

1 s + 1 s ' = 1 f

s ' = s f s - f

Tal que:

f = 1 2 r

Portanto, Aplicando para o s ' :

s ' = 1 2 s r s - 1 2 r

s ' = 1 2 s r 2 s - r 2

Dando uma mexidinha nela pra ficar mais legal de visualizar:

s ' = r s 2 s - r

Agora atenção. Como o espelho é convexo:

f < 0 ⇒ r < 0

Logo, aplicando os valores:

s ' = - 1.2   m 10   m 2 10   m - - 1.2   m

s ' = - 56.6   c m

s ' ≅ - 57   c m

Passo 3

O pior já passou, acredite em mim! No item b) a coisa é de boas! Como a distancia da imagem é negativa:

s ' = - 57   c m

O sinal negativo indica que a imagem está atrás do espelho!

Passo 4

Agora pra finalizar vamos simplesmente calcular a magnificação do espelho, que éda dada pela equação 32.5. Logo, temos:

A = y ' y = - s ' s

Isolando y ' , temos:

y ' = - s ' s y

Substituindo pelos valores numéricos:

y ' = - - 0.566   m 10   m ( 2.0   m )

y ' = 11   c m

Resposta

a )   s ' = - 56.6   c m

b )   A t r á s   d o   e s p e l h o

c )   y ' = 11   c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um milípede está a 1,0 m de distância da parte mais próxima da superfície de uma esfera espelhada com 0,70 m de diâmetro. (a) A que distância da superfície da esfera aparece a imagem do milípede? (b)
A equação 1/p + 1/i = 2/r para espelhos esféricos é uma aproximação que é válida apenas se a imagem for formada por raios que façam pequenos ângulos com o eixo central. Na verdade, muitos ângulos não
Um gafanhoto está no eixo central de um espelho esférico. O valor absoluto da distância focal do espelho é 40,0 cm e a ampliação lateral da imagem produzida pelo espelho é +0,200. (a) O espelho é conv
Uma xícara de chá é posicionada no eixo central de um espelho esférico. A ampliação lateral da xícara é +0,250 e a distância entre o espelho e o ponto focal é 2,00 cm. (a) Qual é a distância entre o e
Um feixe estreito, de raios paralelos, incide em uma esfera de vidro pela esquerda, na direção do centro da esfera. (A esfera se comporta como uma lente, mas certamente não é uma lente delgada.) Supon