Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 10º - Capítulo 7.Problemas - Ex. 51

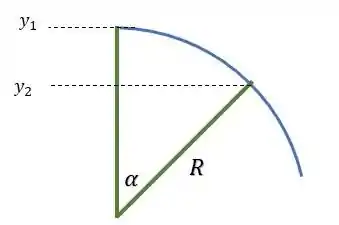
Uma esquiadora parte com velocidade inicial desprezível do topo de uma esfera de neve com raio muito grande e sem atrito e se desloca diretamente para baixo (figura 7.28). Em que ponto ela perde o contato com a esfera e voa seguindo a direção da tangente? Ou seja, no momento em que ela perde o contato com a esfera, qual é o ângulo α entre a vertical e a linha que liga a esquiadora ao centro da esfera de neve?

Passo 1

Beleza pessoal?! Espero que esteja tudo bem com meu os herdeiros de Newton. Vamos dar início a mais uma resolução com o padrão de qualidade do Responde aí, então pegue seu lápis, caderno e café e vamos nessa!!!

K 1 + U 1 + W o u t r a = K 2 + U 2     ( 1 )

Onde a energia cinética é dada por:

K   =   0.5 m v ²     ( 2 )

U g r a v = m g y     ( 3 )

Sabemos, do capítulo 5, que, no movimento circular uniforme, o vetor aceleração é direcionado para o centro do círculo e sua magnitude é dada por:

a r a d = v ² / R     ( 4 )

Passo 2

K 1 = 0

U 1 = 0

K 2 = 0.5 m v ²

U 2 = - m g R ( 1 - c o s α )

Como a força normal está sempre atuando perpendicularmente à direção do movimento, temos:

W o u t r o = 0

0 + 0 + 0 = 0.5 m v ² - m g R ( 1 - c o s α )

v ² = 2 g R ( 1 - c o s α )   R . 1

Aplicamos A segunda lei de Newton ao esquiador ao longo da direção radial, obtemos:

m g   c o s   α = m v ² R

g   c o s   α = v ² R

g c o s   α = 2 g R ( 1 - c o s   α ) R

c o s   α = 2 3

α   =   c o s ⁻ ¹   2 3 = 48.19 ⁰

Resposta

48.19 ⁰

Exercícios de Livros Relacionados

A bala 2 tem duas vezes a massa da bala 1 . As duas são atiradas com a mesma velocidade escalar. Se a energia cinética da bala 1 é K , a energia cinética da bala 2 é 0,25 K , 0,5 K , 0,71 K , K , ou 2
Um jogador de beisebol lança uma bola de 0,150 kg a uma velocidade escalar de 40,0 m/s e um ângulo inicial de 30,0° com a horizontal. Qual é a energia cinética da bola de beisebol no ponto mais alto d
A partícula referente ao exercício 6.16 tem velocidade v = 5m / s quando se encontra na posição x = - 2 m . A) Qual é a velocidade máxima atingida pela partícula? B)Quais são os pontos de retorno da p
Guepardos adultos, os mais rápidos dos grandes felinos, possuem uma massa de aproximadamente 70k g e costumam correr a 32m / s . (a) Quantos joules de energia cinética esse guepardo ligeiro possui? (b
Quando um carro é atingido por trás, seus passageiros sofrem uma aceleração repentina para a frente, que pode causar uma lesão séria no pescoço, conhecida como lesão do “chicote”. Durante a aceleração