Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Serway e Jewett - Física para cientistas e engenheiros - Vol1 - Ed: 1º - Capítulo 7.Problemas - Ex. 55

Um jogador de beisebol lança uma bola de 0,150 kg a uma velocidade escalar de 40,0 m/s e um ângulo inicial de 30,0° com a horizontal. Qual é a energia cinética da bola de beisebol no ponto mais alto de sua trajetória?

Passo 1

Queridos, notem: no ponto mais alto da trajetória, a bola tem velocidade nula na vertical, uma vez que nesse ponto ela para de subir e começa, imediatamente em seguida, a cair.

Por conta disso, nesse ponto, analisando seu movimento na vertical, ela só vai ter energia potencial!

Ainda assim, ela tem velocidade de deslocamento na horizontal, que a gente sabe de outros exercícios de lançamento oblíquo que é sempre constante!

A gente tem a relação entre a velocidade original e as velocidades horizontal e vertical a partir desse esqueminha clássico:

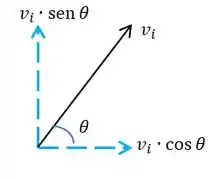
Com isso, sendo a velocidade original v = 40,0   m / s e o ângulo de inclinação de v com a horizontal sendo θ = 30 ° , a gente vai ter pra velocidade horizontal v x :

v x = 40 ∙ cos ⁡ 30 ° = 40 ∙ 3 2

v x = 20 3   m / s

Passo 2

Legal, com isso a gente consegue calcular a energia cinética devida ao movimento da bola, nesse caso, apenas na horizontal.

A partir da formulinha da energia cinética, K = m ∙ v 2 2 , a gente vai ter:

K = 0,150 ∙ 20 3 2 2

K = 0,150 ∙ 40 0 ∙ 3 2

K = 0,450 ∙ 200

∴ K = 90   J

Resposta

K = 90   J

Exercícios de Livros Relacionados

Um asteróide próximo à Terra. Em 13 de abril de 2029 (uma sexta-feira 13!), o asteróide 99942 Apophis passará a 18600m i da Terra – cerca de1 / 3 da distância até a Lua! Ele possui densidade de 2600k
Uma aluna de física gasta parte do seu dia caminhando para se deslocar entre salas de aula ou durante os intervalos e, nesse período, ela gasta energia com uma taxa média de 280 W. No restante do dia
42. Se a energia cinética de uma partícula é igual à sua energia de repouso, qual o erro percentual que se comete ao usar p = m v para sua quantidade de movimento? A expressão não-relativística é semp
45. (a) Mostre que a rapidez v de uma partícula de massa m e energia total E é dada por v / c = [ 1 - ( m c 2 2 ) / 2 E 2 ) ]1 / 2 e que quando E é muito maior que m c 2 , isto pode ser aproximado por
45. (a) Mostre que a rapidez v de uma partícula de massa m e energia total E é dada por v / c = [ 1 - ( m c 2 2 ) / 2 E 2 ) ]1 / 2 e que quando E é muito maior que m c 2 , isto pode ser aproximado por