Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 5.Problemas - Ex. 43
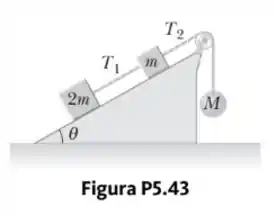
Considere os três corpos conectados, mostrados na Figura P5.43. Assuma primeiro que o plano inclinado não tem atrito e que o sistema está em equilíbrio. Em termos de , e , encontre
a massa e
as tensões e .
Agora, assuma que o valor de é o dobro do encontrado na parte (a). Encontre
a aceleração de cada corpo e
as tensões e .
Em seguida, assuma que o coeficiente de atrito estático entre e e o plano inclinado é , e que o sistema está em equilíbrio. Encontre
o valor máximo de e
seu valor mínimo.
Compare os valores de quando tem seus valores mínimos e máximos.
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo e bora!
Aplicando a segunda lei de Newton a cada objeto, temos:
Passo 2
Letras a e b:
Assumindo que o sistema está em equilíbrio (a = 0) e que a inclinação é sem atrito, as equações reduzem a:
Substituindo [1'] e [3'] na equação [2'], temos:
Então a equação (3') torna-se:
Passo 3
Letras c e d:
(o dobro do valor encontrado acima), e . Com essas condições presentes, as equações tornam-se:
Resolvidos simultaneamente, temos:
Passo 4
Letra e:
Equilíbrio (a = 0) e movimento iminente subindo a inclinação, então enquanto e , ambos direcionados para baixo na inclinação.
Nessas condições, as equações se tornam:
Que nos dá:
Passo 5
Letra f:
Equilíbrio (a = 0) e movimento iminente descendo a inclinação, então enquanto , ambos direcionados para cima na inclinação.
Nessas condições, as equações se tornam:
Que nos dá:
Quando essa expressão dá um valor negativo, isso corresponde fisicamente a uma massa M pendurada em uma corda sobre uma polia na extremidade inferior da inclinação.
Passo 6
Letra g: