Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Exercício - Ex. 11

Em uma experiência no espaço, um próton é mantido fixo e outro próton é libertado do repouso a uma distância de 2,5 mm.

  1. Qual é a aceleração inicial do próton após ser libertado?
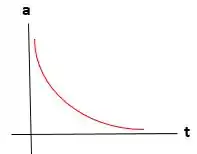
  2. Faça gráficos qualitativos (sem números) da aceleração versus tempo e velocidade versus tempo do movimento do próton libertado.

Passo 1

Para iniciarmos a questão vamos separar alguns dados importates contidos no enunciado.

Q p r ó t o n = Q p = 1,6   x   10 - 19   C

k = 9   x   10 9   N . m 2 / C ²

m p = 1,67   x   10 - 27   k g

r = 2,5   m m = 2,5   x   10 - 3   m

Passo 2

  1. Vamos igualar a força de aceleração com a força elétrica. sendo assim.

    2. F = k Q 1 Q 2 r 2

    m   . a = k | Q p | 2 r 2

    a = k | Q p | ² r 2 .   m

    Substitundo os termos.

    a = 9   x   10 9   . 1,6   x   10 - 19 2 2,5   x   10 - 3 2 .   1 , 67   x   10 - 27

    a = 9   x   10 9   .   2,56   x   10 - 38 6,25   x   10 - 6   .   1,67   x   10 - 27

    a = 23,04   x   10 - 29 10,43   x   10 - 33

    a = 2,2   x   10 4   m / s ²

    Passo 3

  2. A força Elétrica de um único próton em repouso fornece ao próton em movimento a aceleração inicial pela gravidade da Terra. Ou seja, à medida que os prótons se afastam, a força elétrica fica mais fraca e a aceleração diminui. O gráfico que representa a aceleração versus o tempo será.

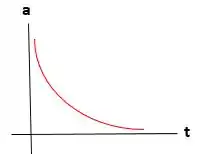
Como os prótons continuam se repelindo (pois suas cargas possuem o mesmo sinal), a velocidade continua aumentando, mas a uma taxa decrescente. O gráfico que representa a velocidade versus o tempo será.

Resposta

  1. a = 2,2   x   10 4   m / s ²

.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Neurônios são componentes do sistema nervoso do corpo que transmitem sinais à medida que impulsos elétricos se propagam ao longo de sua extensão. Essa propagação acontece quando cargas subitamente ent
Uma partícula possui carga igual a - 5,00n C . (a) Determine o módulo, a direção e o sentido do campo elétrico produzido por essa partícula em um ponto situado a 0,250m diretamente acima dela. (b) A q
Um ser humano médio pesa cerca de 650N . Se dois desses seres de peso médio carregassem, cada um, 1,0c o u l o m b de excesso de carga, um positivo e outro negativo, qual deve ser a distância entre el
Duas pequenas esferas separadas por uma distância igual a 20,0c m possuem cargas iguais. Quantos elétrons em excesso devem estar presentes em cada esfera para que o módulo da força de repulsão entre e
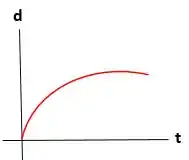
Uma carga negativa de - 0,55 μ C exerce uma força de baixo para cima de 0,600N sobre uma carga desconhecida, situada a 0,300m diretamente abaixo da primeira. (a) Qual é o valor da carga desconhecida (