Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Problemas - Ex. 104d
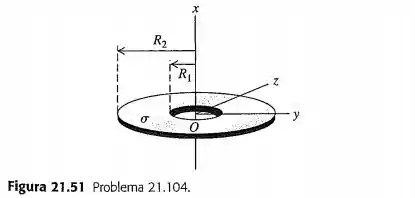
Denomina-se coroa anular um disco fino de raio externo com um buraco circular concêntrico de raio interno (Figura ). Uma coroa anular possui uma densidade superficial de carga sobre sua superfície. Determine a carga total sobre a coroa anular. A coroa anular está sobre o plano com seu centro na origem. Para um ponto arbitrário sobre o eixo (o eixo de simetria da coroa anular), determine o módulo, a direção e o sentido do campo elétrico . Considere todos os pontos acima e abaixo do plano da coroa anular da Figura . Mostre que, para os pontos sobre o eixo suficientemente próximos da origem, o módulo do campo elétrico é aproximadamente proporcional à distância entre o centro da coroa e o ponto considerado. Qual é a distância que pode ser considerada “suficientemente próxima”? Uma partícula puntiforme com massa e carga pode se mover livremente sobre o eixo (mas não pode sair desse eixo). A partícula é inicialmente colocada sobre o ponto e, a seguir, liberada. Determine a frequência das oscilações da partícula. (Sugestão: faça uma revisão da seção . A coroa anular permanece em repouso.)
Passo 1
Dada a informação de que a partícula irá oscilar somente no eixo , isso significa que o seu movimento é do tipo harmônico simples por passar em um ponto de equilíbrio e ser linear.
Lembrando que a frequência do movimento harmônico simples é dado por:
Resta nós encontrarmos qual o valor da variável !
Passo 2
Para tanto, é de nosso conhecimento que a força atuante no MHS é a força elástica da Lei de Hooke:
E, a partir da equação de campo elétrico, a força gerada por ele tem a forma:
Então, igualando ambas as forças:
Concluímos que:
Passo 3
Então, substituindo na equação da frequência, ela vai resultar em: