Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Young and Freedman - Vol 4- Ed: 12º - Capítulo 43.Problemas Desafiadores - Ex. 79

Em uma experiência, o isótopo I 128 é criado irradiando-se o I 127 com um feixe de nêutrons que cria 1,5 × 10 6 núcleos de I 128 por segundo. Inicialmente não existe nenhum núcleo de I 128 presente. A meia-vida do I 128 é 25 minutos.

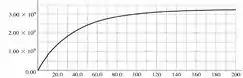
  1. Faça um gráfico do número de núcleos de I 128 presentes em função do tempo.
  2. Qual é a atividade da amostra 1 ,   10 ,   25 ,   50 ,   75 e 180 minutos depois de a irradiação começar?
  3. Qual é o número máximo de I 128 que podem ser criados na amostra depois que ela é irradiada durante um tempo muito longo? (Essa situação estacionária é chamada de saturação).
  4. Qual é a atividade máxima que pode ser produzida?

Passo 1

Letra a)

Aqui temos dois processos acontecendo: a criação do I 128 pela irradiação com um feixe de nêutrons e o decaimento do recém produzido I 128 . Então a expressão de d N / d t terá mais um termo, que vou chamar de K , que é a razão de produção pela irradiação:

d N d t = K - λ N

Então multiplicando dos dois lados por d t e integrando em ambos os lados temos:

d N = ( K - λ N ) d t

Como ( K - λ N ) diz respeito a d N , então vou separar essas duas equações:

d N K - λ N = d t

E integrando temos:

∫ 0 N d N ' K - λ N ' = ∫ 0 t d t

ln ⁡ K - λ N ' 0 N = - λ t

ln ⁡ [ K - λ N ] = ln ⁡ K - λ t

N t = 1 λ K 1 - e - λ t

E o gráfico de N versus t é:

Passo 2

Letra b)

A atividade da amostra é λ N ( t ) , e a partir da expressão que a gente achou na letra anterior temos:

λ N t = K 1 - e - λ t

Com K = 1,5 × 10 6 , e λ que achamos pelo tempo de meia vida, ou seja, λ = 0,693 25 = 0,02772 , para os tempos pedidos, o valor da atividade é só substituir cada um deles aí nessa expressão aí em cima:

  • Para t = 1 m i n :

    • - d N d t = 1,5 × 10 6 1 - e - 0,02772 1 = 4,1 × 10 4 B q

  • Para t = 10 m i n :

    • - d N d t = 1,5 × 10 6 1 - e - 0,02772 10 = 3,6 × 10 5 B q

  • Para t = 25 m i n :

    • - d N d t = 1,5 × 10 6 1 - e - 0,02772 25 = 7,5 × 10 5 B q

  • Para t = 50 m i n :

    • - d N d t = 1,5 × 10 6 1 - e - 0,02772 50 = 1,1 × 10 6 B q

  • Para t = 75 m i n :

    • - d N d t = 1,5 × 10 6 1 - e - 0,02772 75 = 1,3 × 10 6 B q

  • Para t = 180 m i n :

- d N d t = 1,5 × 10 6 1 - e - 0,02772 180 = 1,5 × 10 6 B q

Passo 3

Letra c)

O valor de N m á x vai ser quando e - λ t → 0 , então da expressão que achamos nos itens anteriores temos:

N m á x = K λ = 1,5 × 10 6 0,02772 = 3,2 × 10 9 á t o m o s

Passo 4

Letra d)

A atividade máxima será na saturação, quando a taxa produzida é igual a taxa de decaimento e, portanto, igual a 1,5 × 10 6 d e c a i m e n t o s / s .

Resposta

a )

b ) 4,1 × 10 4 B q ;

3,6 × 10 5 B q ;

7,5 × 10 5 B q ;

1,1 × 10 6 B q ;

1,3 × 10 6 B q ;

1,5 × 10 6 B q .

c ) 3,2 × 10 9 á t o m o s

d ) 1,5 × 10 6 d e c a i m e n t o s / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A radioatividade de uma amostra de Na2 14CO3 foi medida registrando-se o tempo necessário para que a contagem de radiação atingisse 8000. Cinco tempos foram registrados: 21,25; 23,46; 20,97; 22,54; 23
O tecnécio-99m é produzido por uma sequência de radiações em que o molibdênio-98 é bombardeado com nêutrons para formar molibdênio-99, que por sua vez, sofre decaimento β ao tecnécio-99m. (a) Escreva
O actínio-225 decai pela emissão sucessiva de três partículas α. (a) Escreva as equações nucleares dos três processos.
Uma amostra radioativa contem 32P (meia-vida de 14,28 d), 33S (meia-vida de 87,2 d) e 59Fe (meia-vida de 44,6 d). Após 90 dias, uma amostra cuja a massa original era de 8,00 g contém 0,0254 g de 32P,
Se você possui massa média, existem cerca de 360 milhões de núcleos em seu corpo sofrendo decaimento radioativo a cada dia. Expresse sua atividade em curies.