Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Problemas - Ex. 63
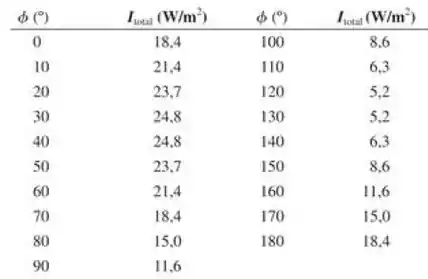
Um feixe de luz propagando-se horizontalmente apresenta um componente não-polarizado com intensidade e um componente polarizado com intensidade . O plano de polarização do componente polarizado forma com a vertical um ângulo igual a . Os dados apresentados a seguir referem-se aos valores da intensidade medidos quando o eixo do polarizador forma com a vertical um ingulo iguala a .a) Qual é a orientacão do componente polarizado (ou seja, qual é o ângulo ). B) Quais são os valores de e ?
Passo 1
Quando a luz incidente é não polarizada, a itensidade após passar pelo polarizador é a metade da intensidade inicial. E quando a luz incidente é polarizada, então a intensiadade depois do polarizador depende do ângulo relativo entre a direção de polarização da luz incidente e do eixo de polarização do polarizador. Ok?
é o ângulo relativo, ou seja:
Vamos usar a tabela agora. Quando , teremos . Pela tabela, a intensidade máxima ocorre quando está entre e . Vamos supor que seja quando . Então
Passo 2
b) agora é só substituirmos os outros valores.
Vamos pegar outra equação para termos um sistema de duas equações. Por exemplo, a configuração de intensidade mínima. Isso ocorre quando .Olhando para a tabela, a intensidade mínima ocorre em
Então
Daqui encontramos que
E então