Considere duas vibrações com a mesma frequência e a mesma amplitude, porém com fases diferentes, uma ao longo do eixo Ox.

E aoutra ao longo do eixo Oy,

As relações anteriores podem ser escritas na forma:

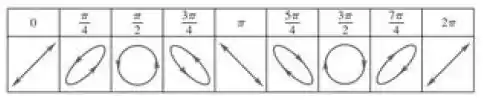
a) Multiplique a Equação (1) por e a Equação (2) por e a seguir subtraia as duas relações resultantes. b) Multiplique Equação (1) por e a Equação (2) por e a seguir subtraia as duas relações resultantes. c) Eleve ao quadrado e some os resultados dos itens (a) e (b). d) Deduza a equação onde . e) Use o resultado anterior para justificar cada um dos diagramas indicados na Figura 33.61. Na figura, o ângulo dado é a diferença de fase entre dois movimentos harmônicos simples com a mesma frequência e com a mesma amplitude, um horizontal (ao longo do eixo Ox) e o outro vertical (ao longo do eixo Oy). Portanto, a figura mostra a superposição de dois movimentos harmônicos simples perpendiculares.

b)

Subtraindo...

Show!

c)

Na letra d, vamos arrumar essa equação.

d)

Pela relação fundamental da trigonometria, , temos:

Usando as relações:

Fazendo

Uhuul!!

e)

Vamos analisar alguns casos. O ângulo mostrado na figura é o .

, temos:

Essa é a equação de uma reta obliqua.

, temos:

Essa é a equação de uma elipse.

, temos:

Essa é a equação de um círculo.