Enunciado
Física - Halliday - Vol 3- Ed: 8º - Capítulo 21.4 - Ex. 8
Na Fig. 21-23, quatro partículas formam um quadrado. As cargas são e (a) Qual deve ser o valor da razão para que a força eletrostática total a que as partículas e estão submetidas seja nula? (b) Existe algum valor de para o qual a força eletrostática a que todas as partículas estão submetidas seja nula? Justifique sua resposta.
Passo 1
Fala aí! como vai? 😊
Nesse problema temos quatro partículas onde e . Queremos saber qual deve ser a razão para que a força eletrostática total a que as partículas e estão submetidas seja nula e tambem se existe algum valor de para o qual a força eletrostática a que todas as partículas estão submetidas seja nula.
Tem ideia de como fazemos isso? 🤔
A dica pra resolver uma questão desse tipo é analisar as forças que atuam sobre cada uma delas. Aqui temos as seguintes cargas: e
Como a letra (a) nos pede para analisar as cargas e , vamos nos concentrar só nelas por enquanto:
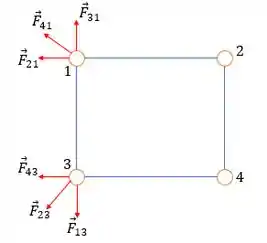
Agora pare e pense: o que precisa acontecer para que as forças resultantes em e sejam diferentes?
Veja que, para isso, é preciso que não hajam componentes de força resultante nem na vertical nem na horizontal em cada um desses pontos. Então vamos fazer ali um somatório de forças e encontrar a tal razão .
Veja só! 😉
Passo 2
Vamos escolher um dos pontos para fazermos o somatório das forças verticais, aqui pegaremos o ponto 1.
Substituindo as equações de força elétrica para as combinações e o valor de cosseno de 45 temos:
Do enunciado, e e também podemos cortar o :
Se a gente dividir geral por chegaremos um pouco mais perto da nossa razão, bora fazer isso?
Opa, tá ali, to vendo a razão! Agora vamos passar alguns termos pro outro lado e multiplicar todo mundo por :
Ih mas o enunciado pediu o inverso!
Show de bolinhas? Vamos pro próximo! 😬
Passo 3
Na letra (a) a gente só analisou as forças atuantes na vertical sobre a partícula . Como o sistema é simétrico na diagonal, repare que a mesma coisa acontece para a partícula . Resta pra gente, então, só analisar uma das partículas ou , já que também existe simetria com relação à diagonal do quadrado.
Fazendo isso, a gente encontra (analisando na direção horizontal a partícula 2):
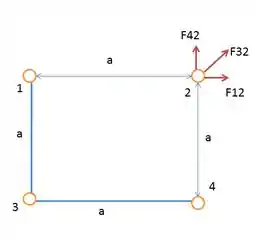
Fazendo o somatório das forças horizontais no ponto 2 temos:
Dividindo essa expressão por e multiplicando ela por , a gente se depara com isso:
Eita! Esse valor é diferente do que o que encontramos no passo 2 (. Isso significa que esse sistema físico não pode ser possível e, portanto, “não existe algum valor de para o qual a força eletrostática a que todas as partículas estão submetidas seja nula”.
E aí! entendeu tudo? Responde Aí! 😊
Resposta
a)
b) Não