Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 3- Ed: 8º - Capítulo 21.4 - Ex. 13

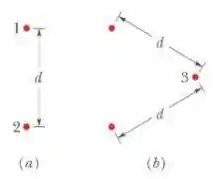
Na Fig. 21-26a as partículas 1 e 2 tem uma carga de 20,0 μ C cada uma e estão separadas por uma distância d = 1.50 m . (a) Qual é o módulo da força eletrostática que a partícula 2 exerce sobre a partícula 1 ? Na Fig. 21-26b, a partícula 3 , com uma carga de 20 μ C , é posicionada de modo a completar um triângulo equilátero. (b) Qual é o modulo da força eletrostática a que a partícula 1 é submetida devido à presença das partículas 2 e 3 ?

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nesse problema temos duas ocasiões para analisar... na primeira temos duas partículas com cargas iguais q = 20 μ C e separadas por uma distância d = 1,5 m . Nosso objetivo a princípio é obter o modulo da força eletrostática que age sobre elas.

Na segunda parte do problema adicionamos uma outra partícula com carga q e distante d de ambas as partículas. Nesse caso queremos obter modulo da força eletrostática sofrida pela partícula 1 .

Lembra como fazemos isso? 🤔

A força eletrostática é calculada pela equação

F e l = K q i q k r 2

Onde K é a constante eletrostática, q i e q k são as cargas das partículas e r a distância entre elas...

Para o caso de termos mais de duas partículas, podemos aplicar o princípio da superposição e calcularmos cada força separadamente...

Veja só! 😁

Passo 2

Vamos começar pelo caso mais simples... quando temos apenas duas cargas...

Nesse caso, basta aplicar os valores na fórmula F e l

F 12 = K q 1 q 2 d 2

Onde K = 9 · 10 9 N m 2 / C 2 , q 1 = q 2 = 20 μ C e d = 1,5 m ...

F 12 = 9 · 10 9 20 · 10 - 6 20 · 10 - 6 1,5 2

F 12 = 1,6 N

Tranquilo até aqui? 😉

Passo 3

Agora para o segundo caso, como as partículas não estão alinhadas no mesmo eixo, temos que calcular cada componente de força separadamente e calcular o modulo posteriormente...

Considerando o eixo y para cima da imagem, já vimos que anteriormente

F 12 = 1,6 j N

Como q 3 = 20 μ C e d = 1,5 m ...

F 1 3 = K q 1 q 3 d 2

F 1 3 = 9 · 10 9 20 · 10 - 6 20 · 10 - 6 1,5 2

F 1 3 = 1,6 N

Podemos obter as componentes x e y de F 13 a partir do ângulo θ do triângulo equilátero.

F 13 x = - F 13 sin ⁡ 60

F 13 y = F 13 cos ⁡ 60

Ou seja

F → 13 = - F 13 sin ⁡ 60 i + F 13 cos ⁡ 60 j N

F → 13 = - 1,6 · 3 2 i + 1,6 · 1 2 j N

F → 13 = - 4 3 5 i + 4 5 j N

Bacana, não é? 😊

Passo 4

Somando as componentes F 12 e F 13 , temos

F 1 → = 1,6 j + - 4 3 5 i + 4 5 j

F 1 → = - 4 3 5 i + 12 5 j N

Calculando o modulo desse vetor...

F 1 = 8 3 5 N

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

F 12 = 1,6 N

F 1 = 8 3 5 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 21-28, as partículas 1 e 2 são mantidas fixas no eixo x , separadas por uma distância L = 8,00c m . As cargas das partículas são q 1 = + e e q 2 = -27 e . A partícula 3 , de carga q 3 = + 4 e
A Fig. 21-34 mostra dois elétrons, 1 e 2 , no eixo x e dois íons, 3 e 4 , de carga - q , no eixo y . O ângulo θ é o mesmo para os dois íons. O elétron 2 está livre para se mover; as outras três partíc
Na Fig. 21-32, as partículas 2 e 4 , de carga -e, são mantidas fixas no eixo y , nas posições y 2=-10,0c m e y 4=5,00c m . As partículas 1 e 3 , de carga -e , podem ser deslocadas ao longo do eixo x .
Um nêutron é composto por um quark "up", com uma carga de + 2 e / 3 , e dois quarks "down", cada um com uma carga de - e / 3 . Se os dois quarks "down" estão separados por uma distância de 2,6 × 10 -
(a) Explique o que acontece com as esferas do Problema 54 se uma delas é descarregada (ligando, por exemplo, momentaneamente a esfera à terra). (b) Determine a nova distância de equilíbrio x , usando