Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.4 - Ex. 9b
Na Fig. 21-24, as cargas das partículas são e . O lado do quadrado é . Determine (a) a componente e (b) a componente da força eletrostática a que está submetida a partícula .
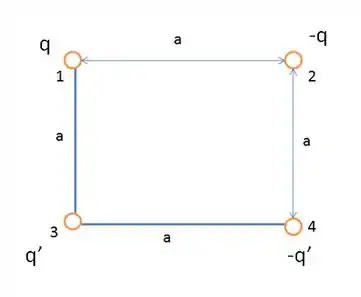
Passo 1
- Para acharmos a força resultante na vertical (componente ) sobre a carga , assim como pede o enunciado, basta a gente somar todas as forças atuantes nessa direção:
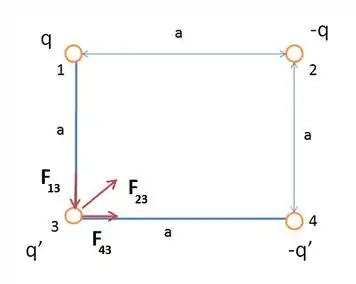
Fazendo isso, a gente encontra a Força resultante :
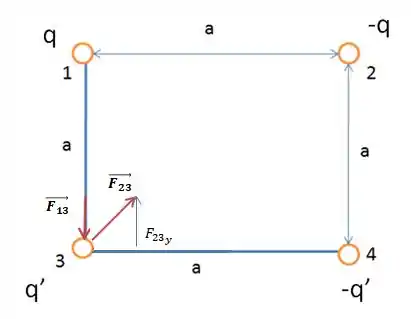
Como aqui nesse caso, temos um quadrado, o ângulo que a força faz é de , pois essa força está na diagonal do quadrado, sendo assim, a sua componente em será:
Passo 2
Agora, é só calcularmos cada um desses caras:
E calculando o outro termo:
E pra finalizar é só somar tudo:
Resposta
(b)
Exercícios de Livros Relacionados
Duas pequenas esferas de alumínio, cada qual com uma massa igual a 0,0025 g, estão separadas por uma distância de 80,0 cm.A que fração da carga total de cada esfera essa quantidade corresponde?
Particulas de um anel de ouro. Você possui um anel de ouro puro (24 quilates) com massa igual a 17,7 g. A massa atômica do ouro é igual a 197 g/mol e seu número atômico é 79. Sabendo que o anel não te
Duas esferas muito pequenas de 8,55 g, estão a uma distância de 15 cm de umcentro a outro e são carregadas adicionando-se um número igual de elétrons a cadauma delas. Desconsiderando-se todas as demai
Uma pequena esfera de chumbo de massa igual a 8,0 g possui excesso de elétrons com uma carga líquida igual a –3,2x10 - 9 C. Calcule o número de elétrons em excesso sobre a esfera.
Duas pequenas esferas de alumínio, cada qual com uma massa igual a 0,0250 kg, estão separadas por uma distância de 80,0 cm.Quantos elétrons estão presentes em cada esfera? (O número atômico do alumíni