Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.4 - Ex. 9a

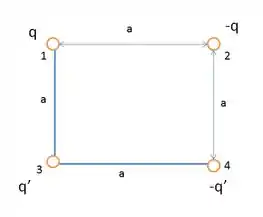
Na Fig. 21-23, as cargas das partículas são q 1   =   - q 2   =   100   n C e q 3   =   -   q 4   =   200   n C . O lado do quadrado é a   =   5,0   c m . Determine (a) a componente x e (b) a componente y da força eletrostática a que está submetida a partícula 3 .

Passo 1

Booom, vamos que vamos, não é?

Nesse problema temos quatro partículas de cargas q 1   =   - q 2   =   100   n C e q 3   =   -   q 4   =   200   n C dispostas nos vértices de um quadrado de lado a = 5 c m . a partir daí queremos obter a componente x da força eletrostática submetida à partícula 3 .

Parece complicado? 🤔

A primeira coisa aqui é desenhar as forças eletrostáticas atuando em 3, como 2 e 4 são negativos a setinha da força apontará para elas, ok? Enquanto a carga 1 é positiva e teremos forças repulsivas atuando:

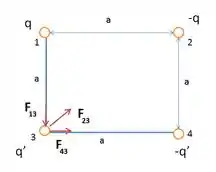
Bom galerinha, no desenho nós podemos observar que a força de 2 sobre 3 está na diagonal, e para dar continuidade vamos precisar do ângulo, ok?

Veja só! 😁

Passo 2

A trigonometria nos diz que:

tan ⁡ θ = C a t e t o   O p o s t o C a t e t e o   A d j a c e n t e = a a = 1

θ = tan - 1 ⁡ 1 = 45 °

Uma outra forma de pensarmos é que esta força aponta na diagonal do quadrado, certo? Portanto ela vai cortar o ângulo de 90° pela metade, o que nos dá 45°!!

Como a força é angular, ou seja, está na diagonal, teremos uma componente em x e em y, certinho?

Então a força resultante deverá ser analisada nestas duas componentes:

F 3 , x = F 43 + F 23 , x = F 43 + F 23 cos ⁡ 45 º

F 3 , y = - F 13 + F 23 , y = - F 13 + F 23 sen ⁡ 45 º

Antes de dar continuidade precisamos obter a distância d entre 3 e 2!!

A trigonometria nos ajuda mais uma fez, já que a distância será igual a hipotenusa de um triângulo retângulo:

d = a 2 + a 2 = 2 a 2 = a 2

Guardemos no coração esta informação !! 😊

Passo 3

E agora? Como calculamos forças eletrostáticas? Acertoooou quem disse Lei de Coulomb!!

Fazendo isso na direção x :

F 3 , x = k q 4 q 3 a 2 + k q 2 | q 3 | a 2 2 2 2

Substituindo K = 8,99 × 10 9 N m 2 / C 2 , q 4 = q 3 = 200 × 10 - 9 C , q 2 = 100 × 10 - 9 C e a = 0,05 m , temos

F 3 , x = 8,99 × 10 9 200 × 10 - 9 200 × 10 - 9 0,05 2 + 8,99 × 10 9 100 × 10 - 9 200 × 10 - 9 ( 0,05 2 ) 2 2 2

F 3 , x = 0,17   N

E com isso achamos a letra (a), bora pra (b)?

E aí! entendeu tudo? Responde Aí! 😉

Resposta

a) 0,17   N .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. abaixo, a partícula 1, de carga -5,00q, e a partícula 2, de carga + 2,00q, são mantidas a uma distância L no eixo x. Se uma partícula 3, de carga desconhecida q 3 , é colocada em um ponto tal
As cargas iniciais das três esferas condutoras iguais a da fig. abaixo são as seguintes: esfera A , Q ; esfera B , - Q / 4 ; esfera C , Q / 2 , em que Q = 2,00 · 1 0 - 14C . As esferas A e B são manti
Dois estudantes de engenharia, João, com uma massa de 90 kg e Maria, com uma massa de 45 kg, estão a 30 m de distância um do outro. Suponha que existam desequilíbrios de carga de 0,01 % nos corpos dos
A soma das cargas de duas pequenas esferas positivamente carregada 5,0x10 - 5C . Se cada esfera é repelida pela outra com uma força eletrostática de 1,0 N e as esferas estão separadas por uma distânci
Um elétron se encontra no vácuo, perto da superfície da Terra, no ponto y = 0 de um eixo vertical. Qual deve ser a coordenada y de um segundo elétron situado no eixo y para que a força eletrostática e