Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 25.5 - Ex. 37

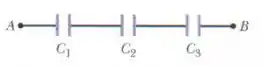
Na figura, C 1 = 10,0 μF, C 2 = 20,0 μF e C 3 = 25,0 μF. Se nenhum dos capacitores pode suportar uma diferença de potencial de mais de 100 V sem que o dielétrico se rompa, determine

(a) a maior diferença de potencial que pode existir entre os pontos A e B;

(b) a maior energia que pode ser armazenada no conjunto de três capacitares.

Passo 1

Letra (a)

A gente sabe que V = q C . A gente também sabe que se eles estão em série, têm a mesma carga q, e o capacitor com menor capacitância vai romper primeiro (porque C vai no denominador). Então vamos olhar parar C 1 :

q = C 1 V 1 = 10,0   μ F 100   V = 1000   μ C

Passo 2

Com essa carga, vamos ver quanto é a ddp nos outros capacitores:

V 2 = q C 2 = 1000   μ C 20,0   μ F = 50,0   V

Agora para o capacitor 3:

V 3 = q C 3 = 1000   μ C 2 5 , 0   μ F = 4 0,0   V

Recapitulando: dos três, o que vai primeiro atingir 100 V é o capacitor 1. Nessa situação, a ddp total é 100,0   V + 5 0,0   V + 4 0,0   V = 1 9 0,0   V

Passo 3

Letra (b)

Vamos usar a fórmula da energia e somar as três energias:

U = 1 2 C 1 V 1 2 + 1 2 C 2 V 2 2 + 1 2 C 3 V 3 2

U = 1 2 1 0 , 0   μ F 10 0,0   V 2 + 1 2 20 , 0   μ F 50,0   V 2 + 1 2 2 5,0   μ F 4 0,0   V 2

U = 95   m J

Resposta

Letra (a): 190 V

Letra (b): 95 mJ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a capacitância equivalente para dois capacitores em série pode ser escrita como C e q = C 1 C 2 C 1 + C 2 Usando apenas esta formula e um pouco de álgebra, mostre que C e q deve ser, sempre
Para o circuito mostrado na Figura 24-36...Os capacitores foram todos descarregados antes de serem conectados à fonte de tensão. Determine (a) a capacitância equivalente da combinação(b) a carga armaz
Determine as diferentes capacitâncias equivalentes que podem ser obtidas usando dois ou três dos seguintes capacitores: um capacitor de 1,00μ F , um capacitor de 2,00µ F µ e um capacitor de 4,00µ F µ
Um capacitor de 20p F é carregado a 3,0k V e, então, removido da bateria e conectado a um capacitor de 50p F descarregado. (a) Qual é a nova carga em cada capacitor? (b) Determine a energia armazenada
Um capacitor de 2,00µ F µ é energizado a uma diferença de potencial de 12,0V . Os fios conectando o capacitor à bateria são, então, desconectados da bateria e conectados a um segundo capacitor que est