Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.Problemas Adicionais - Ex. 54
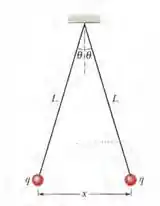
Na Fig. 21-42, duas pequenas esferas condutoras de mesma massa e mesma carga estão penduradas em fios não condutores de comprimento . Suponha que o ângulo é tão pequeno que a aproximação pode ser usada. (a) Mostre que a distância
de equilíbrio entre as esferas é dada por
(b) Se , e , qual é o valor de |?
Passo 1
Turminha do mal, amendrotados? Não criemos pânico, esta aqui é bem legal!! 😉
Nesse problema temos duas pequenas esferas condutoras de mesma massa e mesma carga que estão penduradas em fios não condutores de comprimento . Vamos supor que o ângulo é tão pequeno que a aproximação pode ser usada. A partir daí queremos mostrar que a distância de equilíbrio entre as esferas é dada por
E se , e , temos que calcular o valor de .
Tem ideia de como fazemos isso? 🤔
Mas antes de fazer qualquer coisa nós vamos ampliar este desenho acima inserindo as forças:
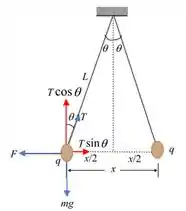
Bom galerinha, vou começar usando a relação que o problema nos disse:
Lembrando lá da trigonometria:
Vamos guardar esta informação, ok?
Veja só! 😬
Passo 2
Agora nós vamos analisar o componente x e y das forças resultantes, assumindo que neste ponto elas estão em equilíbrio:
Lembrando lá da Lei de Coulomb:
A segunda equação fica:
Vamos usar um artifício matemático agora e dividir pelo :
O vai embora e sobra pra gente uma tangente do lado esquerdo!
Se já sabemos o valor da tangente:
Show! Vamos continuar! 😉
Passo 3
Para a letra (b) nós vamos usar:
Colocando na fórmula do Passo 2:
Então:
E fechamos mais umaaa galerinhaa !!
E aí! o que achou? Responde Aí!😊
