Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.Problemas Adicionais - Ex. 44
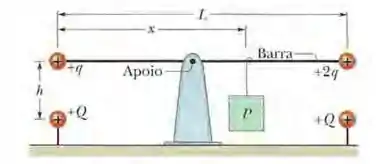
A Fig. 21-44 mostra uma barra longa, não condutora, de massa desprezível, de comprimento , articulada no centro e equilibrada por um bloco de peso situado a uma distância da extremidade esquerda. Nas extremidades direita e esquerda da barra existem pequenas
esferas condutoras de carga positiva e, respectivamente. A uma distância vertical abaixo das esferas existem esferas fixas de carga positiva . (a) Determine a distância para que a barra fique equilibrada na horizontal. (b) Qual deve ser o valor de para que a barra não exerça nenhuma força vertical sobre o apoio quando está equilibrada na horizontal?
Passo 1
Fala aí, galerinha! 😁
Nesse problema temos uma espécie de gangorra onde nas extremidades temos cargas e e abaixo delas temos duas cargas , além disso há um peso em um lado da barra exercendo um torque.
A partir daí queremos determinar a distância para que a barra fique equilibrada na horizontal e tambem queremos saber qual deve ser o valor de para que a barra não exerça nenhuma força vertical sobre o apoio quando está equilibrada na horizontal.
Tem ideia de como fazemos isso? 🤔
Para desolver esse problema podemos lembra da formulinha do torque
Onde é a força aplicada e a distancia até o eixo de rotação.
No caso das cargas, as forças serão calculadas a partir da lei de coulomb, ou seja
Onde é a constante eletrostática, e são as cargas e a distancia entre elas.
Veja só!
Passo 2
Como o sistema está em equilíbrio, podemos usar a equação de equilíbrio de torques (com relação ao apoio) para calcular a distância
Nesse caso, é o torque exercido pela força eletrostática entre e com relação ao eixo, é o torque da força peso e é o torque da força eletrostática entre e .
Isolando nessa equação, a gente encontra:
Tranquilo até aqui? 😉
Passo 3
Agora, pra gente encontrar a força normal que o apoio exerce sobre a barra, temos:
Nesse caso, isolando, , encontramos, finalente:
E aí! entendeu tudo? Responde Aí! 😬
Resposta
a)
b)