Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.9 - Ex. 54

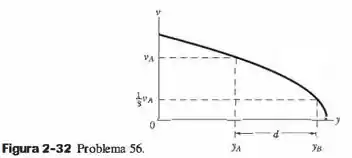
A Fig. 2-32 mostra a velocidade v em função da altura y para uma bola lançada verticalmente para cima ao longo de um eixo y . A distância d é 0,40   m . A velocidade na altura y A é v A . A velocidade na altura y B é v A / 3 . Determine a velocidade v A .

Passo 1

Pessoal, vamos usar a equação de Torricelli para resolver essa questão. Considerando a velocidade inicial v A , a velocidade final v A / 3 e o deslocamento d , teremos que:

v 2 = v 0 2 + 2 g ∆ y

Tal que:

v A 3 2 = v A 2 + 2 g d

Susbituindo os valores na equação, obtemos que:

v A 3 2 = v A 2 + 2 . - 9,8   m/s² . 0,40   m

v A 2 9 - v A 2 = - 7,84   m ² /s²

Portanto:

- 8 9 . v A 2 = - 7,84   m ² /s²

v A 2 = 8,82   m ² /s²

v A = 3,0   m/s

Resposta

R: 3,0   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pedra, largada de um penhasco, cobre um terço da distância total ao solo no último segundo de queda. A resistência do ar é desprezível. Qual é a altura do penhasco?
Uma pedra é atirada verticalmente, para baixo, do topo de um pesnhasco de 200 m. Durante o último meio segundo de seu vôo, a pedra percorre uma distância de 45 m. Encontre a rapidez inicial da pedra.
Um vaso de flores cai do parapeito de um apartamento. Uma pessoa, em um apartamento abaixo, coincidentemente de posse de um sistema de cronometragem ultra-rápido e preciso, percebe que o vaso leva 0,2
Um parafuso se desprende da base de um elevador que está subindo com uma velocidade constande de 6,0 m/s. O parafuso atinge o fundo do poço do elevador em 3,0 s. (a) A que altura do fundo do poço esta
Um objeto é largado do repouso de uma altura h. Durante o último segundo de queda ele percorre uma distância de 38 m. Determine h.