Uma pedra, largada de um penhasco, cobre um terço da distância total ao solo no último segundo de queda. A resistência do ar é desprezível. Qual é a altura do penhasco?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão. Sendo a altura do penhasco e o instante final, isto é, o instante em que a pedra alcança o chão, podemos descrever esses três instantes do movimento:
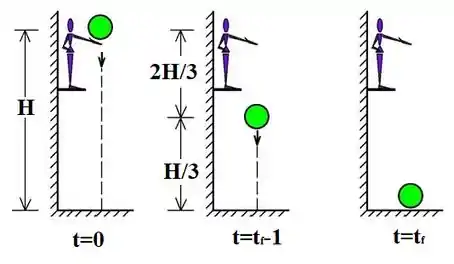
Atenção nesse instante do meio, ok? Como o enunciado falou sobre o último segundo de queda, a gente vai representar ele por:
Afinal, se demorar uns segundos pra isso tudo acontecer, a último segundo não seria o ? Então taí uma forma de representar o último segundo:
Show, dái em diante galera, é só a gente usar nossa querida fórmulinha de Torricelli:
Onde:
- Velocidade final
- Velocidade inicial
- Aceleração
- Posição final
- Posição inicial
Bora então?
Passo 2
Bem galera, vamos usar os dois primeiros instantes então. Vamos ter:
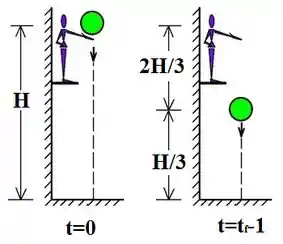
E isso é uma boa ideia porque como a bola sabe do repouso, sabemos a velocidade inicial dela entre esses dois intervalos:
Já facilita a nossa vida, né não? Outros valores que vamos usar em Torricelli pra esses momentos são:
Importante aqui ver que a velocidade e a aceleração são negativas porque apontam pra baixo! Juntando tudo na equação, temos:
Agora vamos usar a mesma ideia, mas considerando esses dois instantes:
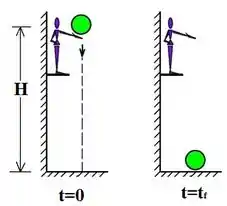
Vamos ter:
E a fórmula fica:
Passo 3
Show galera, parece que ainda não chegamos lá né, mas calma que vai dar bom! Vamos olhar esses dois instantes:
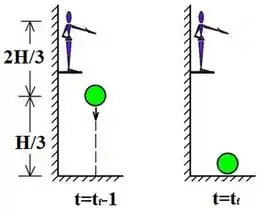
Daqui a gente sabe uma coisa importantíssima: quanto tempo o movimento durou! A da esquerda não é o último segundo e a da direita não é o instante final? Sendo assim:
E considerando que a aceleração da bolinha nesses instantes vai ser:
Pra gente fechar com chave de ouro, basta a gente pegar a expressão de , que na verdade foi o que encontramos no passo anterior! Pro instante inicial nessa referência, temos:
E pro instante final nessa referência:
Ficamos então com:
Elevando os dois lados da última equação ao quadrado, temos:
Pô galera, é a aceleração da gravidade! Um número conhecido! Sendo, aproximadamente:
Temos:
Passo 4
Esse passo aqui é só uma observação galera, na verdade já fechamos a questão! Olha só, daria pra fazer essa questão também usando a fórmula:
Nesse caso, a estratégia seria comparar o primeiro e o segundo instantes pra achar uma equação e o primeiro e terceiro pra achar uma outra equação, ambas em função de e . Essa estratégia faria a gente achar o valor numérico de e, substituindo ele em uma das equações, acharíamos o valor de ! Só pro caso de você ter feito assim, o que também ta super valendo, as equações seriam:
E o valor de encontrado seria: