Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.7 - Ex. 43
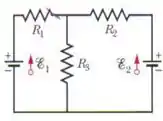
Na Fig. 27-43 , , , , , e as duas fontes são ideais. Determine a potência dissipada (a) em ; (b) em ; (c) em . Determine a potência (d) da fonte 1; (e) da fonte 2.
Passo 1
E aí, pessoal! 😎
Nesse problema temos um circuito com duas fontes e três resistores e são dados , , , , e nosso objetivo é determinar a potência dissipada (a) em ; (b) em ; (c) em . Determine a potência (d) da fonte 1; (e) da fonte 2.
Tem ideia de como fazemos isso? 😉
Para calcular a potência dissipada em um resistor e na fonte, podemos aplicar qualquer uma das equações
Sacou? Então temos que descobrir a corrente e/ou a tensão em cada resistor e na fonte...
Veja só! 😎
Passo 2
Primeiramente, vamos descobrir o valor da corrente. Vamos definir que a corrente tem direção para a direita, a corrente tem sentido para a esquerda e a corrente aponta para cima, dessa forma:
Aplicando a lei das malhas nas duas malhas:
Assim, podemos substituir :
Substituindo na segunda equação:
Isolando ...
Substituindo os valores dados no enunciado...
Portanto a potência dissipada na resistência 1 é :
Tranquilo até aqui? 👀
Passo 3
(b) Podemos encontrar a corrente na resistência 2:
Substituindo os valores dados no enunciado
O sinal negativa mostra que o sentido da corrente é da esquerda para a direita.
E a potência é:
Legal, né? 😊
Passo 4
(c) Podemos achar a corrente na resistência 3:
Se e .
O sinal negativa significa que a corrente está no indo de cima para baixo. E a potência:
Bora lá! 😁
Passo 5
(d) A potência fornecida pela fonte 1 é:
(e) A potência fornecida pela fonte 2 é
O sinal negativo mostra que a fonte está fornecendo energia do sistema.
Entendeu tudo? Respondo Aí! 😉
Resposta
(a)
(b)
(c)
(d)
(e)