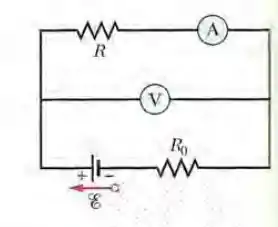
Na Fig. 27-58, um voltímetro de resistência e um amperímetro de resistência estão sendo usados para medir uma resistência R em um circuito que também contém uma resistência e uma fonte ideal de força eletromotriz . A resistência Ré dada por onde V é a diferença de potencial entre os terminais de R e i é a leitura do amperímetro. A leitura do voltímetro é V', que é a soma de V com a diferença de potencial entre os terminais do amperímetro. Assim, a razão entre as leituras dos dois medidores não é R e sim a resistência aparente . Se determine (a) a leitura do amperímetro; (b) a leitura do voltímetro; (c) o valor de R'. (d) Se diminui, a diferença entre R' e R aumenta, diminui ou permanece a mesma?

Aqui temos um circuito em que o voltímetro e o amperímetro possuem resistências internas, que tem que ser levadas em conta no cálculo da corrente e diferença de potencial do circuito.

Para termos a leitura no amperímetro precisamos levar em conta a resistência R e a resistência do voltímetro logo como a corrente no amperímetro é i, a leitura do voltímetro é:

o que nos dá na qual é a resistência aparente. A corrente da fonte é dada por na qual o é a resistencia equivalente da resistência do voltímetro junto com a resistência do amperímetro mais a resistência pois, o amperímetro está em série com a resistência R.

podemos inverter a equação e substituindo os valores da questão

logo substituindo a resistência equivalente a leitura do voltímetro fica: