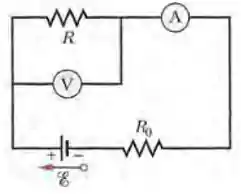
Na Fig. 27-62, um voltímetro de resistência R v = 300 Ω e um amperímetro de resistência R A = 3,00 Ω estão sendo usados para medir uma resistência R em um circuito que também contém uma resistência R 0 = 100 Ω e uma fonte ideal de força eletromotriz ε = 12,0 V . A resistência R é dada por R = V i , onde V é a leitura do voltímetro e i é a corrente na resistência R . Entretanto, a leitura do amperímetro não é i e sim i ' , que é a soma de i com a corrente no voltímetro. Assim, a razão entre as leituras dos dois medidores não é R e sim a resistência aparente R ' = V i ' . Se R = 85,0 Ω , delermine (a) a leitura do amperímetro; (b) a leitura do voltímetro; (c) o valor de R ' . (d) Se R v aumenta, a diferença entre R ' e R aumenta, diminui ou permanece a mesma?

(a) i ’ = 7,09 × 10 - 2 (b) V = 4,70 V . (c) R ’ = 66,3 Ω (d) diminui

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.8 - Ex. 56

Na Fig. 27-62, um voltímetro de resistência e um amperímetro de resistência estão sendo usados para medir uma resistência em um circuito que também contém uma resistência e uma fonte ideal de força eletromotriz . A resistência é dada por , onde é a leitura do voltímetro e é a corrente na resistência . Entretanto, a leitura do amperímetro não é e sim , que é a soma de com a corrente no voltímetro. Assim, a razão entre as leituras dos dois medidores não é e sim a resistência aparente . Se , delermine (a) a leitura do amperímetro; (b) a leitura do voltímetro; (c) o valor de . (d) Se aumenta, a diferença entre e aumenta, diminui ou permanece a mesma?

Passo 1

Fala aí! tudo certinho? 😬

Temos um circuito onde não temos um amperímetro e nem voltímetro ideais, logo para saber a leitura temos que saber a resistência aparente

Essa resistência será a resistência equivalente entre o resistor e o voltímetro e como estão em paralelo podemos usar produto sobre soma.

Vamos passar aqui por um processo de reduzir esse circuito misto num circuito em série, daí calcularemos a resistência equivalente e com isso as outras componentes, ok?

Saca só! 😉

Passo 2

Começando por aplicando o produto sobre soma temos:

Como e temos:

E para fazer a resistência equivalente do circuito é só somar tudo já que transformamos essa parcela paralela em série.

Tranquilo até aqui? 😎

Passo 3

a) Com a resistência equivalente poderemos calcular a leitura do amperímetro sabendo que , temos:

(b) A leitura do voltímetro podemos tirar fazendo:

Isso por quê a voltagem daquele conjunto deve ser a mesma voltagem da resistência equivalente do conjunto multiplicada pela corrente que passa por lá, então é só a gente substituir os valores que já calculamos:

Bacana, não é? 😇

Passo 4

(d) Se aumenta, a diferença entre e diminui pois desta equação quanto maior o maior o logo a diferença diminui

E aí! o que achou? Responde Aí! 😁

Resposta

(a)

(b)

(c)

(d) diminui

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 29-13, suponha que E = 5.0 V. r = 2.0 Ω, R1 - 5,0 Ω e R2= 4,0 Ω. Sabendo-se que a resistência do amperímetro é RA = 0,10 Ω, que erro percentual é cometido na leitura da corrente? Suponha que o

Um capacitor C inicialmente descarregado é plenamente carregado por um dispositivo de fem constante E em série com um resistor R. (a) Mostre que a energia final armazenada no capacitor é metade da ene

Um voltímetro (resistência Rv) e um amperímetro (resistência RA) são ligados para medir uma resistência R, como mostra a Fig. 29-43a. A resistência é dada por R= V/i, onde V é a leitura do voltímetro

Para o controle manual, sensível da corrente num circuito, podemos usar uma combinação em paralelo de resistores variáveis do tipo contato deslizante, como mostra a Fig. 29-39. Suponhamos que a resist

Quando as luzes de um automóvel são ligadas, um amperímetro em série com elas indica 10 A e um voltímetro ligado através delas indica 12 V. Veja a Fig. 29-42. Quando o motor de arranque é ligado, a in