Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 27.Problemas Adicionais - Ex. 105
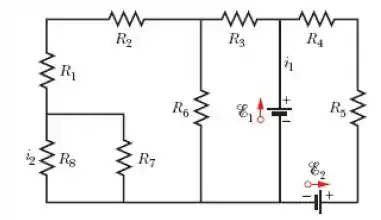
Na Fig. 27-84, e as forças eletromotrizes das fontes são e . Determine:
(a) o valor absoluto e
(b) o sentido (para cima ou para baixo) da corrente , e
(c) o valor absoluto e
(d) o sentido (para cima ou para baixo) da corrente.
Determine a potência fornecida ou absorvida
(e) pela fonte 1 e
(f) pela fonte 2.
(g) A fonte 1 está fornecendo ou absorvendo energia?
(h) A fonte 2 está fornecendo ou absorvendo energia?
Passo 1
Letra a:
Vamos por partes aqui! Vamos ver quanto da corrente chega na resistência . A corrente some e se divide igualmente, pois a resistência vale e a resistência equivalente do outro fio (que é a soma das resistências e ) também dá .
Então na resistência passa .
Daí esse fio saem outros dois fios, que passam pelas resistências e . E as resistências equivalentes desses dois fios também são iguais, pois . As resistências e estão em paralelo, cada uma vale , então a equivalente entre elas vale a metade, ou seja, . Somando com as e dá .
Então no fio de passa a metade da corrente (que já estava dividida pela metade) de entrada, ou seja, .
E do outro lado também! Nas resistências e a corrente é e como há uma associação em paralelo entre as e , ali a corrente vai se dividir novamente igualmente, ficando para cada lado. Então chegamos a conclusão de que .
Mas e a Bom, vamos pela malha bem da direita, que passa pelas duas fontes e pelos resistores e . Sabemos as correntes neles, e sabemos a tensão, então indo pelo sentido horário temos:
Passo 2
Letra b: como encontramos uma corrente positiva, o sentido que assumimos no passo anterior está correto: o sentido de é para cima.
Passo 3
Letra c:
O valor absoluto de já sabemos, pois ele está relacionado com :
Passo 4
Letra d:
O sentido da corrente já sabemos, e não é preciso fazer nenhuma conta. Quando fomos distribuindo a corrente já colocamos um sentido no circuito todo. Assumimos o sentido anti horário para o circuito e portanto é para baixo. Como o sentido de está correto com o que nós assumimos no começo, o sentido de também.
Passo 5
Letra e:, a potência da fonte é a multiplicação da corrente pela tensão, então para a fonte temos:
Passo 6
Letra f: lembrando que a corrente que passa na fonte é , a potência da fonte vai ser:
Passo 7
Letra g: a fonte está fornecendo energia, pois a corrente que passa por ele está indo do pólo de menor potencial para o de maior potencial.
Passo 8
Letra h: já a fonte está absorvendo energia, pois a corrente está fluindo nela do pólo positivo para o negativo.