Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 27.Problemas Adicionais - Ex. 100
Na Fig. 27-81, as forças eletromotrizes das fontes ideais são e , e todas as resistências são de . Determine
(a) o valor absoluto e
(b) o sentido (para a direita ou para a esquerda) da corrente e
(c) o valor absoluto e
(d) o sentido (para a direita ou para a esquerda) da corrente .
(Sugestão: O problema pode ser resolvido de cabeça.)
(e) Qual é a potência fornecida ou recebida pela fonte ?
(f) A fonte está fornecendo ou recebendo energia?
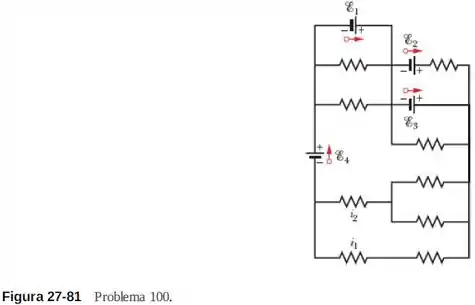
Passo 1
Parece complicado, mas não é! Dá pra fazer de cabeça mesmo! Vamos usar a lei das malhas e fazer um caminho que seja bem tranquilo! A ideia aqui é identificar um caminho que tenha a corrente que queremos, passe por várias fontes e pelo menor número de resistências possíveis. Bora lá?
Letra a:
Dá uma espiadela no caminho em laranja aqui embaixo:
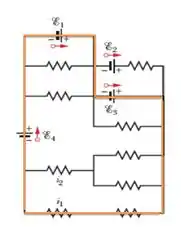
Esse caminho passa pelas fontes e e por duas resistências (em série) e daí temos a corrente . Pela lei das malhas temos:
Passo 2
Letra b:
E o sentido é para a esquerda.
Passo 3
Letra c:
Agora vamos ver outro caminho, saca só esse aqui de baixo:
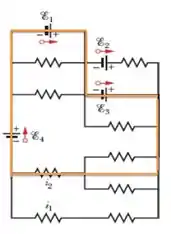
Ele passa por três fontes e por uma associação em paralelo (que a resistência equivalente já sabemos é a medade do valor de uma delas, já que elas são iguais) ligada a uma resistência em série que passa por . Usando a lei das malhas temos:
Passo 4
Letra d: e o sentido é o anti horário, ou seja, a corrente vai para a esquerda.
Passo 5
Letra e:
A corrente total que passa pela fonte é a soma das duas correntes que encontramos, então:
E a potência é a tensão multiplicada pela corrente:
Passo 6
Letra f: ela está fornecendo energia, já que o sentido da corrente é positivo.