Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 28.Problemas Adicionais - Ex. 89

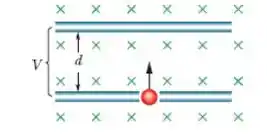
Na Fig. 28-58, um elétron de massa m, carga e velocidade inicial perpendicular ao plano da

placa superior, penetra em uma região entre duas placas separadas por uma distância e submetidas a uma diferença de potencial , com uma velocidade inicial perpendicular ao plano da placa superior. Na região entre as placas existe um campo magnético de módulo que aponta para dentro do papel. Considerando a velocidade inicial do elétron tão pequena que pode ser desprezada, determine o menor valor de para o qual o elétron não se choca com a placa superior.

Passo 1

Como a velocidade inicial do elétron pode ser desprezada, no início temos apenas energia potencial e ela deve ser toda convertida em energia cinética:

Passo 2

Quando o elétron penetra nessa região entre as placas, a força magnética ele sofre é igual a força centrípeta. Para que ele não se choque na placa superior, o raio da trajetória deve ser , assim igualando as forças temos:

Passo 3

Daí substituindo a velocidade na expressão da energia lá do passo 1 e substituindo por temos:

E simplificando teremos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma certa partícula subatômica decai em um elétron e um pósitron. Suponha que, no instante do decaimento, a partícula está em repouso em um campo magnético uniforme B → de módulo 3,53 m T e que as tra

Uma linha de transmissão horizontal é percorrida por uma corrente de 5000A no sentido sul-norte. O campo magnético da Terra ( 60,0 μ T ) tem a direçāo norte e faz um ângulo de 70 , 0 ∘ c o m a horizon

Uma partícula descreve um movimento circular uniforme com 26,1 μ m de raio em um campo magnético uniforme. O módulo da força magnética experimentada pela partícula é 1,60 × 10 - 17 N. Qual é a energia

Prove que a relação τ = N i A B s e n ⁡ θ não é válida apenas para a espira retangular da Fig. 28-19, mas também para uma espira fechada com qualquer forma geométrica. (Sugestão: substitua a espira de

Estime a distância total percorrida por um dêuteron em um cíclotron com um raio de 53c m e uma frequência de operação de 12 M H z durante todo o processo de aceleração. Suponha que a diferença de pote