Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.4 - Ex. 22

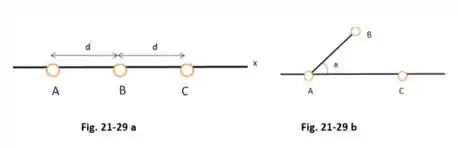
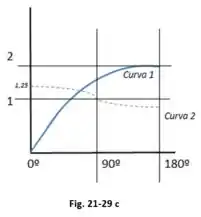
A Fig. 21-29a mostra um sistema de três partículas carregadas separadas por uma distância . As partículas e estão fixas num lugar no eixo , mas a partícula pode se mover ao longo de uma circunferência com centro na partícula . Durante o movimento, um segmento de reta ligando os pontos e faz um ângulo com o eixo (Fig. 21-29b). As curvas da Fig. 21-29c mostram, para dois valores diferentes da razão entre a carga da partícula e a carga da partícula , o módulo , da força eletrostática total que as outras partículas exercem sobre a partícula . A força total foi plotada em função do ângulo e como múltiplo da uma força de referência . Assim, por exemplo, na curva , para , vemos que .

(a) Nas condições em que foi obtida a curva , qual é a razão entre a carga da partícula e a carga da partícula (incluindo o sinal)? (b) Qual é a razão nas condições em que foi obtida a curva ?

Passo 1

Fala aí, pessoal! 😬

Nesse problema temos um sistema de três partículas carregadas separadas por uma distância sendo as partículas e fixas no eixo , mas a partícula pode se mover ao longo de uma circunferência com centro na partícula .

A partir daí queremos obter a razão entre a carga e a carga na curva 1 e na curva 2.

Tem ideia de como fazemos isso? 😐

Primeiro, vamos analisar as condições extremas, em que e por que elas representam situações em que a força total é máxima e mínima.

Como a força eletrostática é proporcional ao inverso da distância ao quadrado e as distância entre a partícula e a partícula é o dobro da distância entre e , então a força entre e seria quatro vezes menor que a força entre e , caso as cargas e fossem iguais.